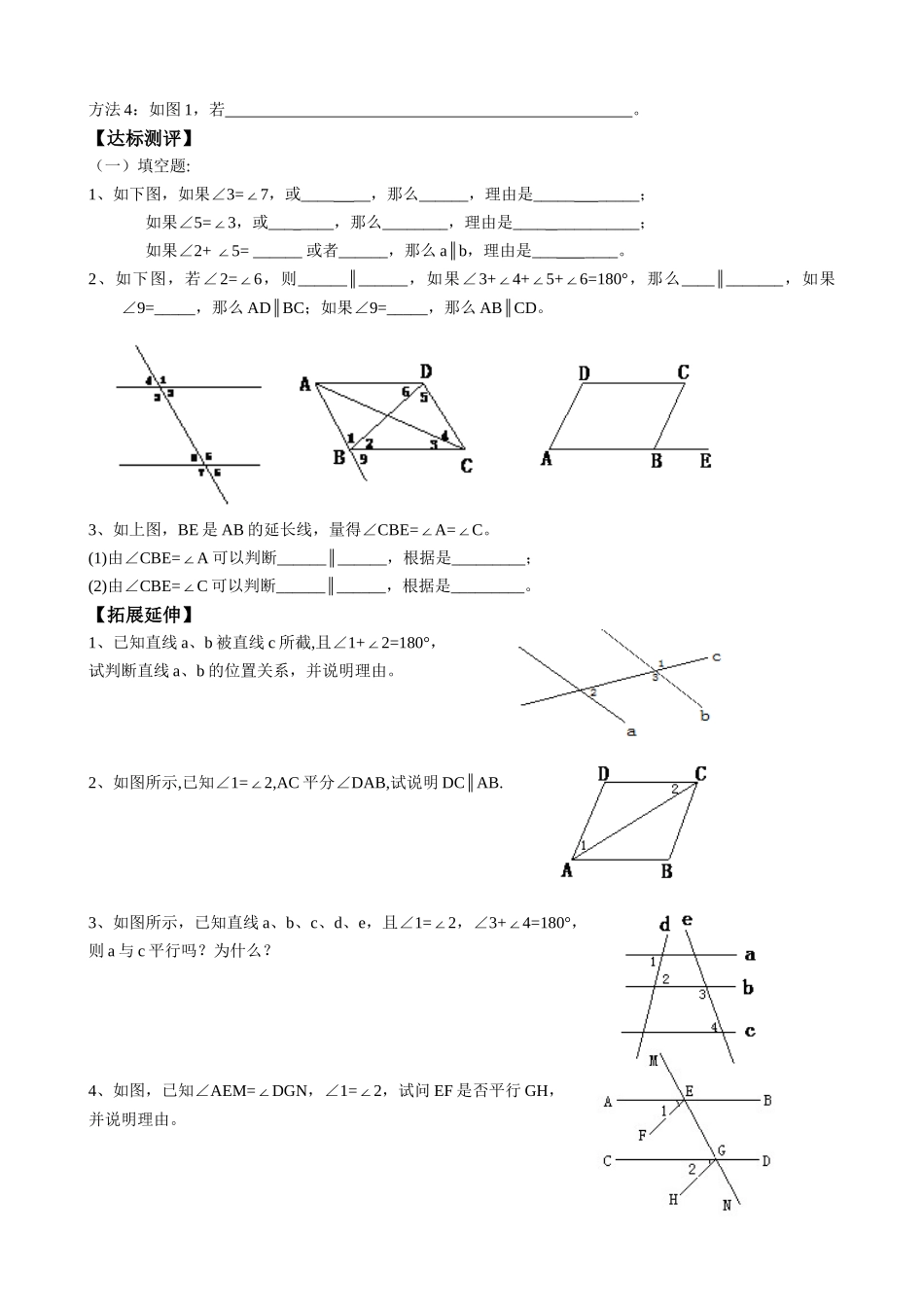
5.2.2平行线的判定第一课时【学习目标】1、使学生掌握平行线的四种判定方法,并初步运用它们进行简单的推理论证。2、初步学会简单的论证和推理,认识几何证明的必要性和证明过程的严密性。【学习重点】在观察实验的基础上进行公理的概括与定理的推导【学习难点】定理形成过程中的逻辑推理及其书面表达。【学具准备】三角板【自主学习】1、预习疑难:。2、填空:(1)平行线的定义:在同一平面内,的两条直线叫做平行线。(2)平行公理:经过直线外一点,________与这条直线平行。(3)平行公理的推论:的两直线平行。应用格式:∵ab∥,bc∥ac∴∥(平行于同一直线的两直线平行)【合作探究】(一)平行线判定方法1:1、观察思考:过点P画直线CDAB∥的过程,三角尺起了什么作用?图中,∠1和∠2什么关系?2、判定方法1:简单说成:。应用格式:∵∠1=∠2(已知)ABCD∴∥(同位角相等,两直线平行)3、应用:木工师傅使用角尺画平行线,有什么道理?(二)平行线判定方法2、3:1、思考:教材13页(试着写出推理过程)判定方法2:简单说成:。应用格式:∵∠2=∠3(已知)ab∴∥(内错角相等,两直线平行)2、将上题中条件改变为∠2+∠4=180°,能得到ab∥吗?(试写出推理过程)判定方法3:简单说成:。应用格式:∵∠2+∠4=180°(已知)ab∴∥(同旁内角互补,两直线平行)【反馈提高】(一)练一练:教材14页练习1、2、3(二)总结直线平行的条件:方法1:若ab∥,bc∥,则ac∥。即平行于同一直线的两直线平行。方法2:如图1,若∠1=∠3,则ac∥。即。方法3:如图1,若。方法4:如图1,若。【达标测评】(一)填空题:1、如下图,如果∠3=7∠,或______,那么______,理由是__________;如果∠5=3∠,或_______,那么________,理由是______________;如果∠2+5=______∠或者______,那么ab∥,理由是_______。2、如下图,若∠2=6∠,则____________∥,如果∠3+4+5+6=180°∠∠∠,那么___________∥,如果∠9=_____,那么ADBC∥;如果∠9=_____,那么ABCD∥。3、如上图,BE是AB的延长线,量得∠CBE=A=C∠∠。(1)由∠CBE=A∠可以判断____________∥,根据是_________;(2)由∠CBE=C∠可以判断____________∥,根据是_________。【拓展延伸】1、已知直线a、b被直线c所截,且∠1+2=180°∠,试判断直线a、b的位置关系,并说明理由。2、如图所示,已知∠1=2,AC∠平分∠DAB,试说明DCAB.∥3、如图所示,已知直线a、b、c、d、e,且∠1=2∠,∠3+4=180°∠,则a与c平行吗?为什么?4、如图,已知∠AEM=DGN∠,∠1=2∠,试问EF是否平行GH,并说明理由。