抛物线几何性质1VIP免费

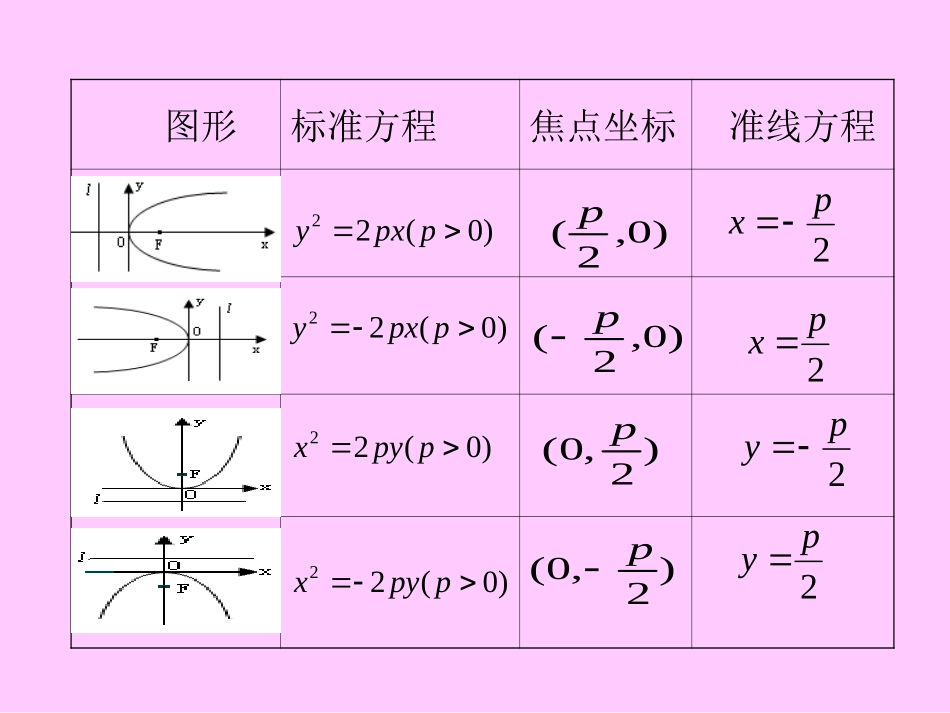
抛物线的简单几何性质施教者:夏伟峰1、抛物线的定义:知识回顾2、抛物线的标准方程)0(2),0(2)0(2),0(22222ppyxppyxppxyppxy图形标准方程焦点坐标准线方程)0(22ppxy)0,2(p2px)0(22ppxy)0(22ppyx)0(22ppyx)0,2(p)2,0(p)2,0(p2px2py2py葡萄美酒夜光杯,欲饮琵琶马上催.问题1:如果测量得酒杯杯口宽4cm，杯深8cm，试求出该抛物线方程？4cm8cm背景引入4cm8cm解：如图建立平面直角坐标系,则可知A(-2,8),B(2,8)所以设抛物线的方程为：A、B点在抛物线上，代入抛物线方程，可得P=,则所求的抛物线方程为：)0(22ppyx41.212yx方程范围对称轴顶点离心率yx2120yy轴(0,0)e=1问题2：研究酒杯轴截面所在曲线的几何性质。引申：探照灯反射镜的轴截面是抛物线的一部分。已知灯口圆的直径为60cm，灯深40cm，则光源的位置在_____________处，光线最亮。BFAOFABxy所以光源在垂直灯口直径且距探照灯顶点处845解：如图，在探照灯的轴截面所在平面内建立平面直角坐标系，是反光镜的顶点（即抛物线的顶点）与原点重合，x轴垂直于灯口直径。设抛物线的标准方程是由已知条件可得A（40，30），代入方程，得所以所求的抛物线的标准方程是焦点为).0(22ppxy445p).0,845(,2452xy图形标准方程焦点坐标准线方程顶点对称轴离心率)0(22ppxy)0,2(p2px)0(22ppxy)0(22ppyx)0(22ppyx)0,2(p)2,0(p)2,0(p2px2py2py(0,0)x轴e=1(0,0)(0,0)(0,0)x轴y轴y轴e=1e=1e=1练习西湖隧道的横断面由抛物线弧及一个矩形的三边围成，尺寸如图（单位：m），一辆卡车空车时能通过此隧道，现载一集装箱，箱宽3m，车与箱共高4.5m，此车能否通过隧道？并说明理由。623xA(-3,-3)623yoB(3,-3)CD解:如图,建立坐标系,则A(-3,-3),B(3,-3).设抛物线方程为将B点代入,得.抛物线方程为因为车和箱共高4.5米,则集装箱上表面距抛物线型隧道拱顶0.5米.设抛物线上的D点的坐标为(x0,-0.5),)0(22ppxx23p)03(32xyx.36||2||.26.230020xCDxx所以故此车不能通过隧道.例1：过抛物线的焦点F的直线与抛物线相交于A,B两点,自A、B向准线作垂线,垂足分别为C、D,求证:90CFD)0(22ppxy90CFD)0(22ppxy例1：过抛物线的焦点F的直线与抛物线相交于A,B两点,自A、B向准线作垂线,垂足分别为C、D,求证:１２５３４６证明：如图，由抛物线定义知|AF|=|AC|,所以。同理，。又AC//BD，因为所以则，可证AFCACFBDFBFD180BDFBFDAFCACF180DBFCAF90BFDAFC90CFD变式1若在上题的条件中,以线段CD为直径的圆有与点F有什么关系?MN小结：主要通过抛物线型酒杯研究抛物线的几何性质及应用.体现了数形结合的解析几何思想.