高中数学选修2-2：113　导数的几何意义VIP免费

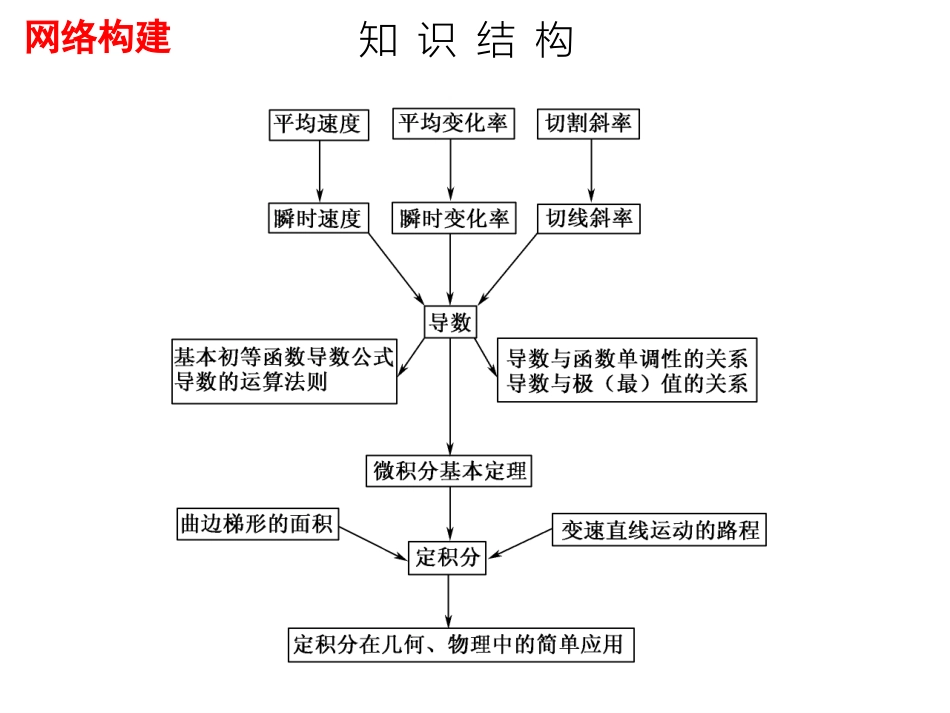
第一章导数及其应用知识结构网络构建学案1.通过函数的图象直观地理解导数的几何意义．2．会求函数在点(x0，y0)处的切线方程.基础梳理1．导数的几何意义(1)割线斜率与切线斜率设函数y＝f(x)的图象如图所示，AB是过点A(x0，f(x0))与点B(x0＋Δx，f(x0＋Δx))的一条割线，此割线的斜率是ΔyΔx＝fx0＋Δx－fx0Δx.当点B沿曲线趋近于点A时，割线AB绕点A转动，它的极限位置为直线AD，这条直线AD叫做此曲线在点A处的____．于是，当Δx→0时，割线AB的斜率无限趋近于过点A的切线AD的斜率k，即k＝______＝__________________.切线f′(x0)limΔx→0fx0＋Δx－fx0Δx基础梳理(2)导数的几何意义函数y＝f(x)在点x＝x0处的导数的几何意义是曲线y＝f(x)在点P(x0，f(x0))处的切线的____．也就是说，曲线y＝f(x)在点P(x0，f(x0))处的切线的斜率是_______．相应地，切线方程为______________________．2．函数的导数当x＝x0时，f′(x0)是一个确定的数，则当x变化时，f′(x)是x的一个函数，称f′(x)是f(x)的导函数(简称导数)．f′(x)也记作y′，即f′(x)＝y′＝____________________.斜率f′(x0)y－f(x0)＝f′(x0)(x－x0)limΔx→0fx＋Δx－fxΔx拓展延伸1.“函数f(x)在点x0处的导数”、“导函数”、“导数”三者之间的区别与联系：“函数f(x)在点x0处的导数”是一个数值；“导函数”简称“导数”，是一个函数．所以求函数在某点处的导数时，一般是先求出函数的导函数，再计算这点的导函数值．拓展延伸2．可以利用导数求曲线的切线方程．由于函数y＝f(x)在x＝x0处的导数，表示曲线在点P(x0，f(x0))处的切线的斜率．因此，曲线y＝f(x)在点P(x0，f(x0))处的切线方程可如下求得：(1)求出f′(x0)，则f′(x0)就是点P(x0，f(x0))处的切线的斜率．(2)代入直线的点斜式方程可得切线方程为y－f(x0)＝f′(x0)(x－x0)．如果曲线y＝f(x)在点P(x0，f(x0))处的切线平行于y轴时(此时导数不存在)，切线方程为x＝x0.巩固提高【例1】已知曲线C：y＝x3.(1)求曲线C上横坐标为1的点处的切线方程；(2)第(1)小题中的切线与曲线C是否还有其他的公共点．巩固提高【解】(1)将x＝1代入曲线C的方程得y＝1，∴切点P(1,1)． y′＝limΔx→0ΔyΔx＝limΔx→0x＋Δx3－x3Δx＝limΔx→03x2Δx＋3xΔx2＋Δx3Δx＝limΔx→0[3x2＋3xΔx＋(Δx)2]＝3x2，巩固提高∴y′|x＝1＝3.∴过P点的切线方程为y－1＝3(x－1)，即3x－y－2＝0.巩固提高(2)由y＝3x－1＋1，y＝x3可得(x－1)(x2＋x－2)＝0，解得x1＝1，x2＝－2，从而求得公共点为P(1,1)或P(－2，－8)．说明切线与曲线C的公共点除了切点外，还有另外的公共点．巩固提高【例2】求抛物线y＝x2过点(52，6)的切线方程．巩固提高【解】设此切线在抛物线上的切点为(x0，x20)，则y′|x＝x0＝limΔx→0x0＋Δx2－x20Δx＝limΔx→0(2x0＋Δx)＝2x0，∴x20－6x0－52＝2x0，即x20－5x0＋6＝0，解得x0＝2，或x0＝3.即切线经过抛物线y＝x2上的点(2,4)，(3,9)．巩固提高故切线方程分别为y－4＝4(x－2)，y－9＝6(x－3)，即4x－y－4＝0，或6x－y－9＝0为所求的切线方程．巩固提高【例3】抛物线y＝x2在点P处的切线与直线4x－y＋2＝0平行，求P点的坐标及切线方程．巩固提高【解】设P点的坐标为(x0，y0)， y′＝limΔx→0ΔyΔx＝limΔx→0x＋Δx2－x2Δx＝limΔx→0(2x＋Δx)＝2x，∴y′|x＝x0＝2x0.由切线与直线4x－y＋2＝0平行，得2x0＝4，∴x0＝2. P(2，y0)在抛物线y＝x2上，∴y0＝4.故P点的坐标为(2,4)．切线方程为y－4＝4(x－2)，即4x－y－4＝0.巩固提高【例4】求曲线y＝x2在点(3,9)处的切线与两坐标轴所围成的三角形的面积．巩固提高【解】Δy＝(3＋Δx)2－32＝6Δx＋(Δx)2，∴f′(3)＝limΔx→0ΔyΔx＝limΔx→0(6＋Δx)＝6.∴点(3,9)处的切线方程为y－9＝6(x－3)，即y＝6x－9.切线与两坐标轴的交点分别为(32，0)，(0，－9)．∴切线与两坐标轴围成的三角形面积为S＝12×32×9＝274.课堂练习1.设曲线y＝ax2在点(1，a)处的切线与直线2x－y－6＝0平行，则a等于()A．1B.12C．－12D．－1课堂练习解析f′(1)＝limΔx→0ΔyΔx＝limΔx→0a...