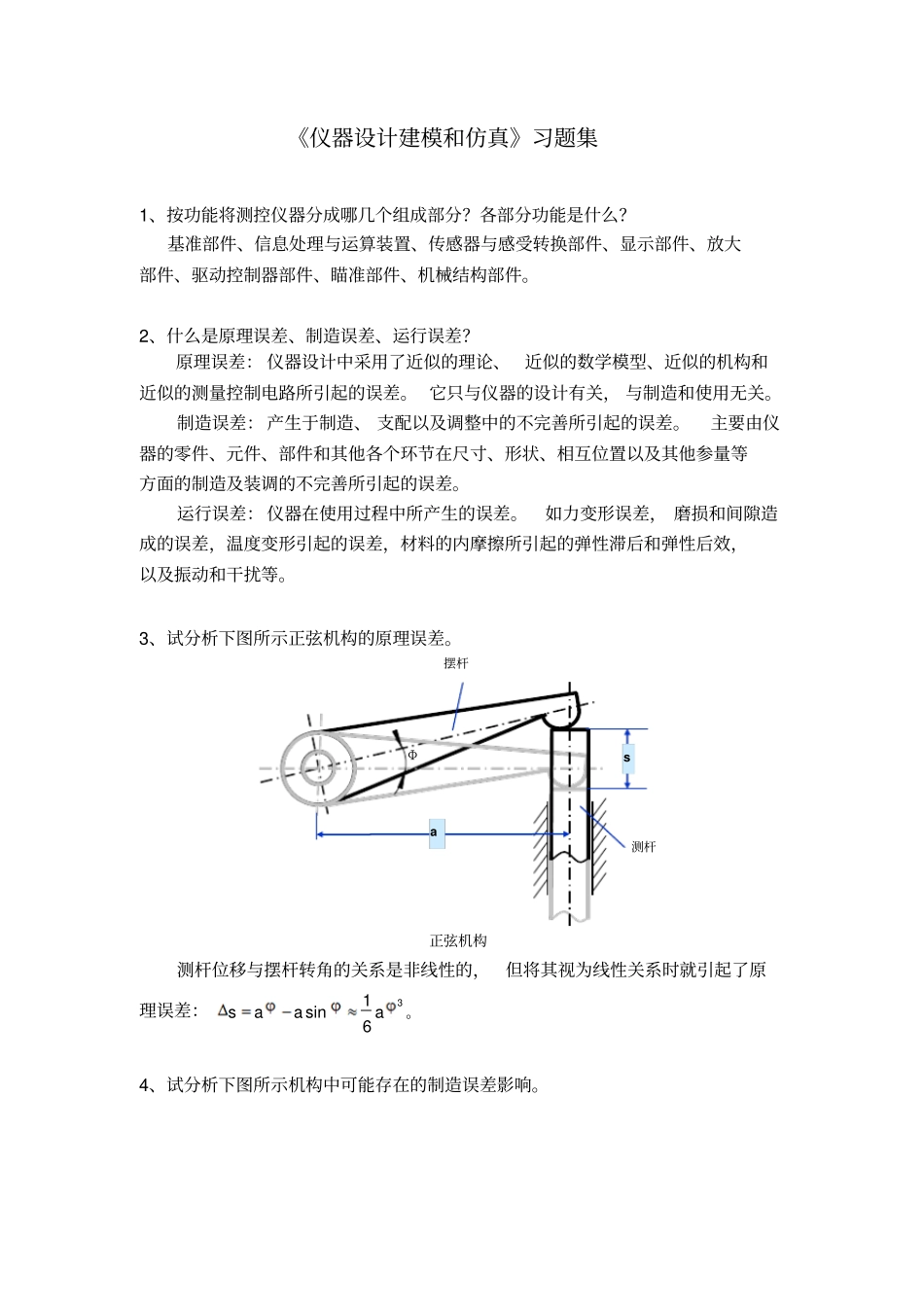
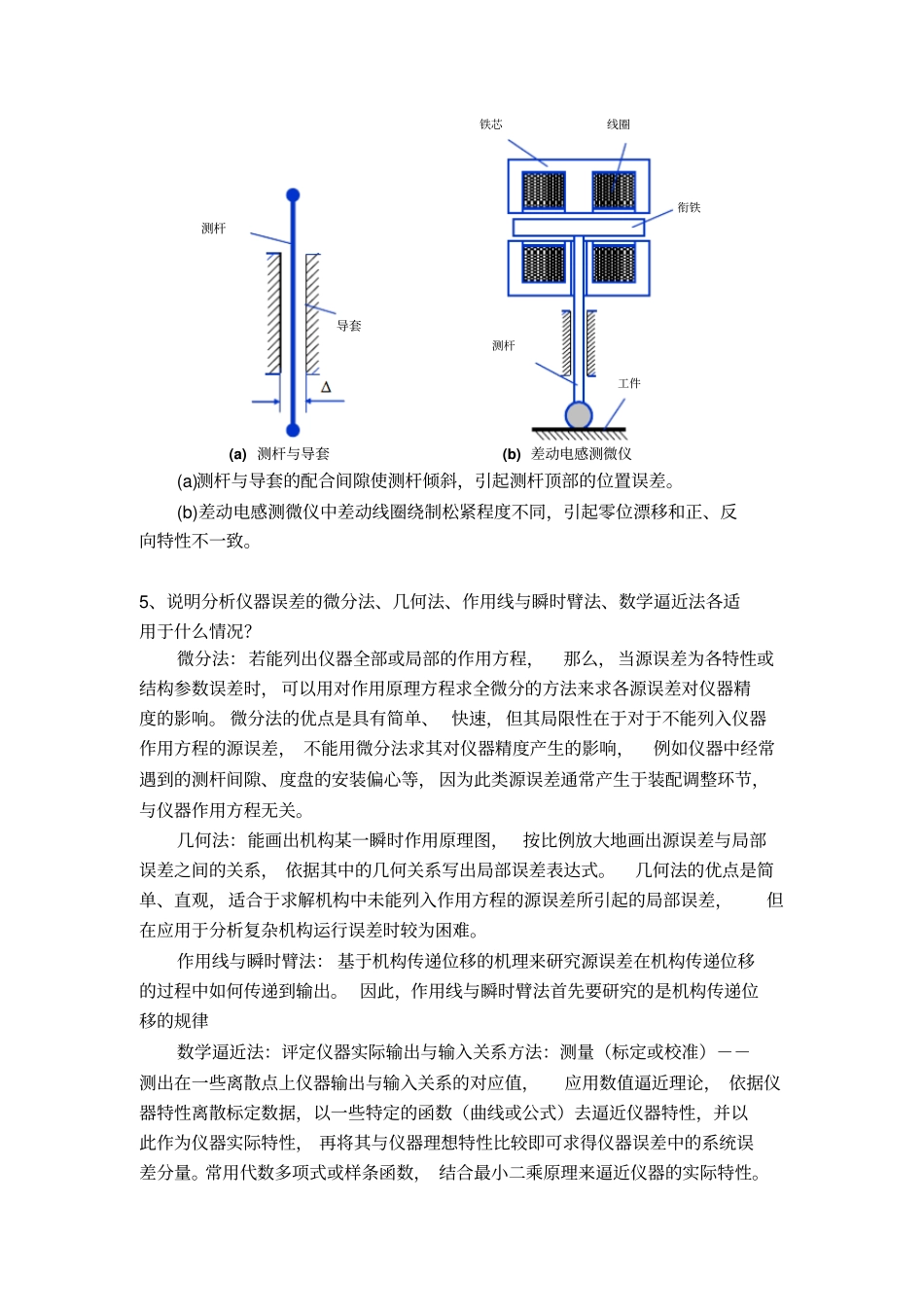
《仪器设计建模和仿真》习题集1、按功能将测控仪器分成哪几个组成部分?各部分功能是什么?基准部件、信息处理与运算装置、传感器与感受转换部件、显示部件、放大部件、驱动控制器部件、瞄准部件、机械结构部件。2、什么是原理误差、制造误差、运行误差?原理误差:仪器设计中采用了近似的理论、近似的数学模型、近似的机构和近似的测量控制电路所引起的误差。它只与仪器的设计有关,与制造和使用无关。制造误差:产生于制造、支配以及调整中的不完善所引起的误差。主要由仪器的零件、元件、部件和其他各个环节在尺寸、形状、相互位置以及其他参量等方面的制造及装调的不完善所引起的误差。运行误差:仪器在使用过程中所产生的误差。如力变形误差,磨损和间隙造成的误差,温度变形引起的误差,材料的内摩擦所引起的弹性滞后和弹性后效,以及振动和干扰等。3、试分析下图所示正弦机构的原理误差。正弦机构测杆位移与摆杆转角的关系是非线性的,但将其视为线性关系时就引起了原理误差:361sinaaas。4、试分析下图所示机构中可能存在的制造误差影响。sΦa摆杆测杆(a)测杆与导套(b)差动电感测微仪(a)测杆与导套的配合间隙使测杆倾斜,引起测杆顶部的位置误差。(b)差动电感测微仪中差动线圈绕制松紧程度不同,引起零位漂移和正、反向特性不一致。5、说明分析仪器误差的微分法、几何法、作用线与瞬时臂法、数学逼近法各适用于什么情况?微分法:若能列出仪器全部或局部的作用方程,那么,当源误差为各特性或结构参数误差时,可以用对作用原理方程求全微分的方法来求各源误差对仪器精度的影响。微分法的优点是具有简单、快速,但其局限性在于对于不能列入仪器作用方程的源误差,不能用微分法求其对仪器精度产生的影响,例如仪器中经常遇到的测杆间隙、度盘的安装偏心等,因为此类源误差通常产生于装配调整环节,与仪器作用方程无关。几何法:能画出机构某一瞬时作用原理图,按比例放大地画出源误差与局部误差之间的关系,依据其中的几何关系写出局部误差表达式。几何法的优点是简单、直观,适合于求解机构中未能列入作用方程的源误差所引起的局部误差,但在应用于分析复杂机构运行误差时较为困难。作用线与瞬时臂法:基于机构传递位移的机理来研究源误差在机构传递位移的过程中如何传递到输出。因此,作用线与瞬时臂法首先要研究的是机构传递位移的规律数学逼近法:评定仪器实际输出与输入关系方法:测量(标定或校准)--测出在一些离散点上仪器输出与输入关系的对应值,应用数值逼近理论,依据仪器特性离散标定数据,以一些特定的函数(曲线或公式)去逼近仪器特性,并以此作为仪器实际特性,再将其与仪器理想特性比较即可求得仪器误差中的系统误差分量。常用代数多项式或样条函数,结合最小二乘原理来逼近仪器的实际特性。测杆铁芯线圈衔铁工件测杆导套6、激光干涉测长仪的光路图如下图所示。其测量方程为:)(20cmLLnKL若测量开始时计数器“置零”,在理想情况下,有nKL20。已知仪器中的源误差包括:测量环境的变化如温度、湿度、气压等,使空气折射率发生变化n、激光波长发生变化0;测量过程中由于测量镜的移动导致仪器基座受力状态发生变化,使测量光路与参考光路长度差发生改变)(cmLL;计数器的计数误差K。试分析各源误差引起的仪器总误差。激光干涉测长仪光路图根据微分法,源误差引起的仪器误差:)()()(22202000cmcmLLnnKKLLLnnKnKKnL7、由于制造或装配的不完善,使得螺旋测微机构的轴线与滑块运动方向成一夹角,如下图所示。试分析由此引起的滑块位置误差。螺旋测微机构示意图螺杆移动距离为:PL2滑块的移动距离:cos2cosPLL滑块位置误差:cos22PPLLL8、下图所示,分析测杆与导套之间的配合间隙所引起的作用误差。测杆与导套为摩擦传动作用副,作用线为导套中心线,由于两者之间存在间隙使测杆倾斜h,引起的作用误差可按几何关系折算为2)cos1(2LLF导轨弹簧滑块滚珠螺旋副手轮9、下图所示摩擦盘直尺运动副,其原始误差有摩擦盘直径误差ΔD=0.005mm,摩擦盘回转偏心e=0.002mm。当摩擦盘转角从0o转到30o时,求作用误差。摩擦盘直尺运动副回转偏心作用误差:eededrFe2)cos1(sin)(max...