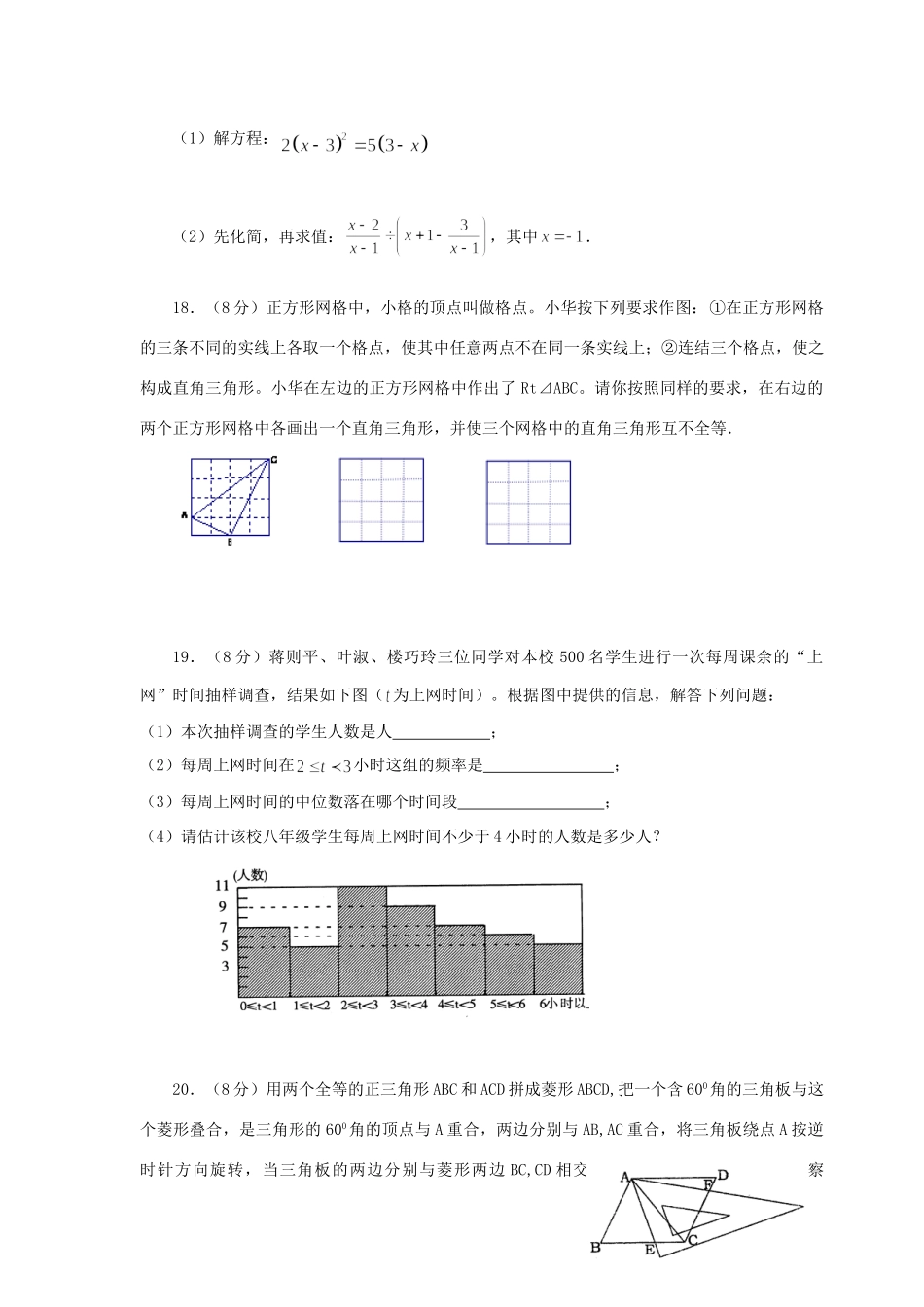
2006年下学期九年级数学月考试卷第Ⅰ卷一、选择题(每小题4分,共40分)1.一元二次方程的根是A.B.C.D.2.下列运算正确的是A.B.C.D.3.点M(2,-3)关于y轴的对称点N的坐标是A.(-2,-3)B.(-2,3)C.(2,3)D.(-3,2)4.下列图形:线段、正三角形、平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形,其中既是中心对称图形,又是轴对称图形的共有A.3个B.4个C.5个D.6个5.右图是甲、乙两组数据的折线统计图,下列结论中正确的是A.甲组数据比乙组数据稳定B.乙组数据比甲组数据稳定C.甲、乙两组数据一样稳定D.不能比较两组数据的稳定性6.下列命题是真命题的是A.有一个角是直角的四边形是矩形B.有一组邻边相等的四边形是菱形C.有三个角是直角的四边形是矩形D.有三条边相等的四边形是菱形7.等边三角形的高为2,则它的面积是A.2B.4C.D.48.如图,一束光线从y轴上点A(0,1)出发,经过x轴上一点C反射后经过点B(3,3),则光线从A点到B点经过的路线长是A.5B.6C.2D.39.一个均匀的立方体各面上分别标有数字1,2,3,4,6,8,其216438表面展开图是如图所示,抛掷这个立方体,则朝上一面的数字恰好等于朝下一面上的数字的2倍的概率是A.B.C.D.10.如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有A.4个B.5个C.6个D.7个第Ⅱ卷二、填空题(每小题5分,共30分)11.不等式组的解是___▲___.12.分解因式:a3-2a2+a=___▲___.13.如图,,,,,则▲.14.如图1,,要使,则需要补充一个条件,这个条件可以是___▲____.(只需填写一个,不再添加线)15.如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是___▲____.16.以下的(1)(2)两题,每个考生只须选答一题,如果两题都答,只以第(1)题计分[第(1)题答对得3分;第(1)题不答,第(2)题答对得5分](1)等腰三角形腰上的高线等于腰长的一半,则这个等腰三角形的顶角等于___▲___度.(2)△ABO中,OA=OB=5,OA边上的高线长为4,将△ABO放在平面直角坐标系中,使点O与原点重合,点A在x轴的正半轴上,那么点B的坐标是____▲____.三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17.(每小题4分,共8分)(1)解方程:(2)先化简,再求值:,其中.18.(8分)正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等.19.(8分)蒋则平、叶淑、楼巧玲三位同学对本校500名学生进行一次每周课余的“上网”时间抽样调查,结果如下图(为上网时间)。根据图中提供的信息,解答下列问题:(1)本次抽样调查的学生人数是人;(2)每周上网时间在小时这组的频率是;(3)每周上网时间的中位数落在哪个时间段;(4)请估计该校八年级学生每周上网时间不少于4小时的人数是多少人?20.(8分)用两个全等的正三角形ABC和ACD拼成菱形ABCD,把一个含600角的三角板与这个菱形叠合,是三角形的600角的顶点与A重合,两边分别与AB,AC重合,将三角板绕点A按逆时针方向旋转,当三角板的两边分别与菱形两边BC,CD相交于点E、F时,通过测量或观察BE、CF的长度,你能得出什么结论?并证明你的结论.21.(10分)三人相互传球,由甲开始发球,并作为第一次传球.⑴用列表或画树状图的方法求经过3次传球后,球仍回到甲手中的概率是多少?⑵由⑴进一步探索:经过4次传球后,球仍回到甲手中的不同传球的方法共有多少种?⑶就传球次数与球分别回到甲、乙、丙手中的可能性大小,提出你的猜想(写出结论即可).22.(12分)已知:CD为一幢3米高的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方A点处建一幢12米高的楼房AB(...