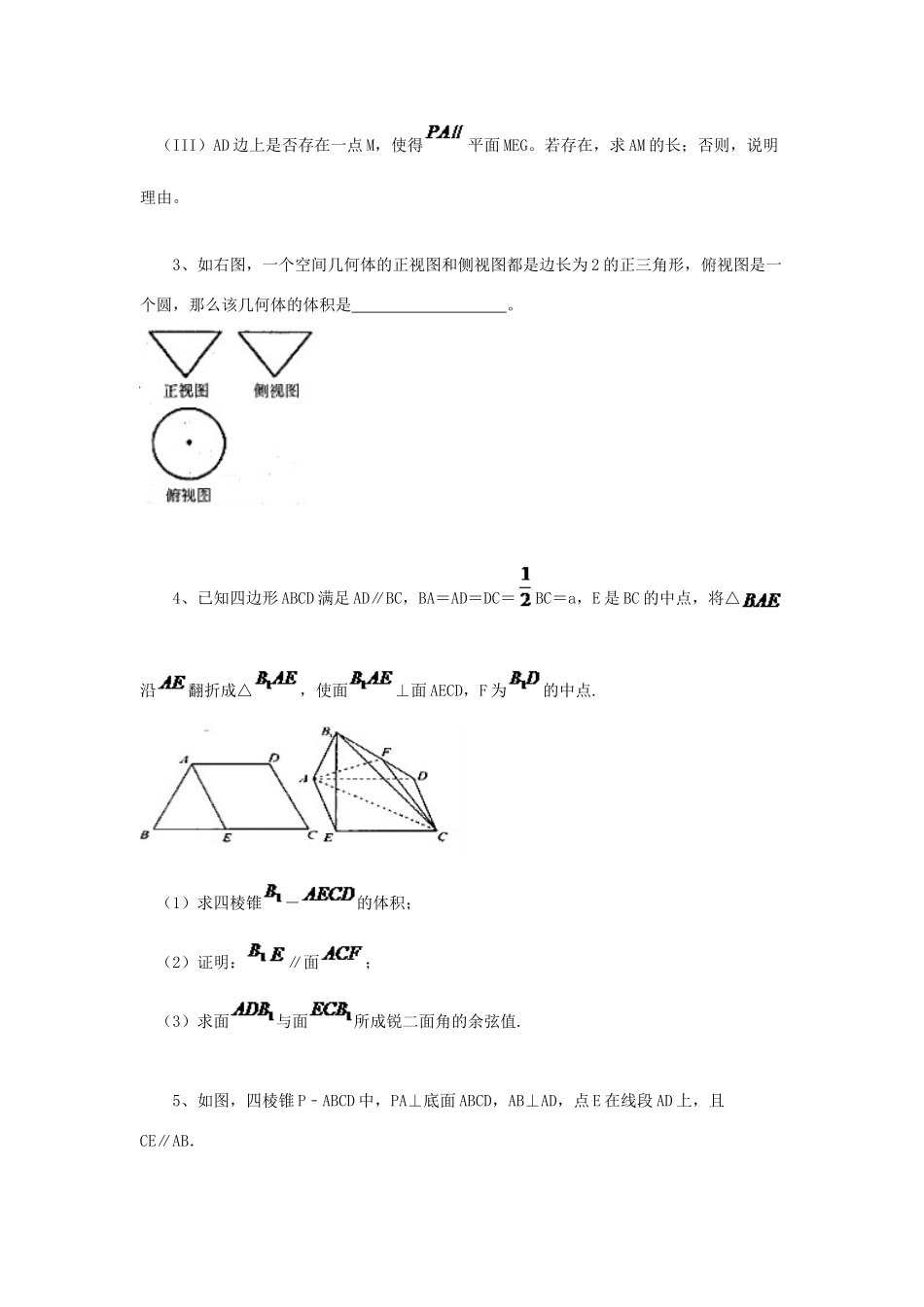
空间几何体的表面积与体积练习1、一空间几何体按比例绘制的三视图如图所示,则该几何体的体积为()m3A.B.C.D.2、如图,四棱锥P—ABCD中,平面ABCD,底面为正方形,BC=PD=2,E为PC的中点,(I)求证:(II)求三棱锥C—DEG的体积;(III)AD边上是否存在一点M,使得平面MEG。若存在,求AM的长;否则,说明理由。3、如右图,一个空间几何体的正视图和侧视图都是边长为2的正三角形,俯视图是一个圆,那么该几何体的体积是。4、已知四边形ABCD满足AD∥BC,BA=AD=DC=BC=a,E是BC的中点,将△沿翻折成△,使面⊥面AECD,F为的中点.(1)求四棱锥-的体积;(2)证明:∥面;(3)求面与面所成锐二面角的余弦值.5、如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.(Ⅰ)求证:CE⊥平面PAD;(Ⅱ)若PA=AB=1,AD=3,CD=,∠CDA=45°,求四棱锥P﹣ABCD的体积.(Ⅲ)在满足(Ⅱ)的条件下求二面角B﹣PC﹣D的余弦值的绝对值.6、已知几何体A-BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,已知几何体A-BCED的体积为16.(1)求实数a的值;(2)将直角三角形△ABD绕斜边AD旋转一周,求该旋转体的表面积.7、如图一所示,四边形ABCD为等腰梯形,AD∥BC,AD=4,BC=8,O、O1分别为BC、AD的中点,将梯形ABOO1沿直线OO1折起,使得平面ABOO1⊥平面OO1DC,得到如图二所示的三棱台AO1D﹣BOC,E为BC的中点.(1)求证:BC⊥平面OO1E;(2)若直线O1E与平面ABCD所成的角的正弦值为,求三棱锥A﹣BOC的体积.8、某几何体的三视图如图所示,则它的体积是()A.B.C.8﹣2πD.9、若某几何体的三视图如图所示,则此几何体的体积是.10、如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P﹣DCE三棱锥的外接球的体积为()A.B.C.D.11、某几何体的三视图如图所示,则该几何体的体积为()A.12B.24C.30D.4812、一个几何体的三视图如图所示,则该几何体的体积的是()A.B.C.D.713、一个四面体的顶点都在球面上,它们的正视图、侧视图、俯视图都是右图.图中圆内有一个以圆心为中心边长为1的正方形.则这个四面体的外接球的表面积是()A.πB.3πC.4πD.6π14、如图是一个几何体的三视图,则该几何体体积为()A.15B.16C.17D.1815、如图,菱形的边长为,现将沿对角线折起至位置,并使平面平面.(Ⅰ)求证:;(Ⅱ)在菱形中,若,求直线与平面所成角的正弦值;(Ⅲ)求四面体体积的最大值.16、如图,在长方体中,,沿该长方体对角面将其截成两部分,并将它们再拼成一个新的四棱柱,那么这个四棱柱表面积的最大值为___________.17、一个几何体的三视图如图所示,其中俯视图与侧视图均为半径为2的圆,则这个几何体的表面积是()A.B.C.D.18、某三棱锥的三视图如图所示,则该三棱锥的各个面中,最大的面积是()A.B.1C.D.19、如图,三角形ABC中,AC=BC=,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.(Ⅰ)求证:GF∥底面ABC;(Ⅱ)求证:AC⊥平面EBC;(Ⅲ)求几何体ADEBC的体积V.20、端午节即将到来,为了做好端午节商场促销活动,某商场打算将进行促销活动的礼品盒重新设计.方案如下:将一块边长为10的正方形纸片剪去四个全等的等腰三角形再将剩下的阴影部分折成一个四棱锥形状的包装盒,其中重合于点O,与重合,与重合,与重合,与重合(如图所示).(Ⅰ)求证:平面平面;(Ⅱ)当时,求二面角的余弦值.答案1、A2、(I)证明:平面ABCD,…………1分又 ABCD是正方形,∴BC⊥CD,…………2分 PDICE=D∴BC⊥平面PCD又 PC面PBC∴PC⊥BC…………4分(II)解: BC⊥平面PCD,∴GC是三棱锥G—DEC的高。…………5分 E是PC的中点,……6分…………8分(III)连结AC,取AC中点O,连结EO、GO,延长GO交AD于点M,则PA//平面MEG。…………9分下面证明之 E为PC的中点,O是AC的中点,∴EO//平面PA,…………10分又∴PA//平面MEG…………11分在正方形ABCD中, O是AC中点,≌∴所求AM的长为…………12分3、4、(1)取AE...