高二数学上学期盟校期末考试试题 文-人教版高二全册数学试题VIP免费

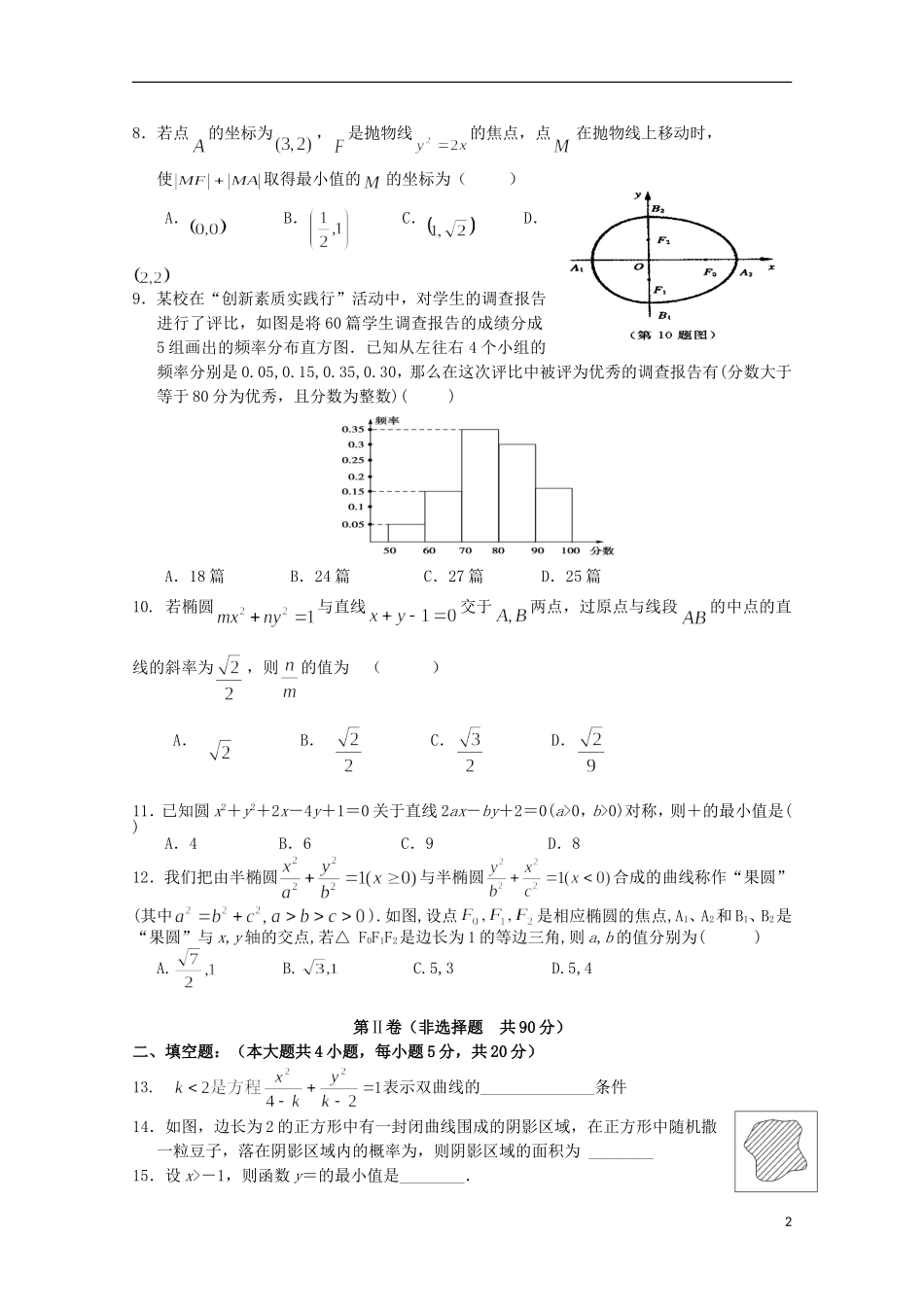
2014—2015学年度第一学期盟校期末联考高二数学（文科）考生注意：1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分。考试时间120分钟。2.请将各题答案填在试卷后面的答题卡上。第Ⅰ卷（选择题共60分）一．选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中只有一项是符合题目要求的）．1．函数y＝8x＋(x>0)的最小值是()A．2B．3C．8D．102．“x＝1”是“(x－1)(x－2)＝0”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．即不充分也不必要条件3．抛物线y＝x2的准线方程是（）A．y＝1B．y＝－1C．x＝－1D．x＝14．命题：“若12x，则11x”的逆否命题是（）A．若12x，则11xx，或B．若11x，则12xC．若11xx，或，则12xD．若11xx，或，则12x5．下列给出的赋值语句正确的是()A．6＝AB．M＝－MC．B＝A＝2D．x＋5y＝06．从1,2,3,4,5,6这6个数字中，不放回任取两数，两数都是偶数的概率是()A．B．C．D．7．如图所示，程序框图的输出结果是()A．4B．6C．5D．318．若点的坐标为，是抛物线的焦点，点在抛物线上移动时，使取得最小值的的坐标为（）A．B．C．D．9．某校在“创新素质实践行”活动中，对学生的调查报告进行了评比，如图是将60篇学生调查报告的成绩分成5组画出的频率分布直方图．已知从左往右4个小组的频率分别是0.05,0.15,0.35,0.30，那么在这次评比中被评为优秀的调查报告有(分数大于等于80分为优秀，且分数为整数)()A．18篇B．24篇C．27篇D．25篇10.若椭圆与直线交于两点，过原点与线段的中点的直线的斜率为，则的值为（）A．B．C．D．11．已知圆x2＋y2＋2x－4y＋1＝0关于直线2ax－by＋2＝0(a>0，b>0)对称，则＋的最小值是()A．4B．6C．9D．812．我们把由半椭圆与半椭圆合成的曲线称作“果圆”(其中).如图,设点是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角,则a,b的值分别为()A.B.C.5,3D.5,4第Ⅱ卷（非选择题共90分）二、填空题：（本大题共4小题，每小题5分，共20分）13.表示双曲线的______________条件14．如图，边长为2的正方形中有一封闭曲线围成的阴影区域，在正方形中随机撒一粒豆子，落在阴影区域内的概率为，则阴影区域的面积为________15．设x>－1，则函数y＝的最小值是________．2116．已知椭圆，使得对于直线，椭圆上有不同的两点关于该直线对称，则的取值范围为___________．三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤.)17．(本题满分10分)已知命题p：x∈[1,2]，x2－a≥0，命题q：x0∈R，x＋2ax0＋2－a＝0.若命题“p∧q”是真命题，求实数a的取值范围。18．(本题满分12分)一箱方便面共有50包，从中用随机抽样方法抽取了10包称量其重量(单位：g)结果为：60.561606061.559.559.5586060(1)指出样本数据的众数、中位数、平均数；(2)求样本数据的方差．19．(本题满分12分)将一颗质地均匀的正方体骰子先后抛掷两次，记第一次出现的点数为x，第二次出现的点数为y.(1)求事件“x＋y<4”的概率；(2)求事件“|x－y|＝3”的概率．20．(本题满分12分)某房地产开发公司计划在一楼区内建造一个长方形公园ABCD，公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成．已知休闲区A1B1C1D1的面积为4000m2，人行道的宽分别为4m和10m.求：(1)若设休闲区的长A1B1＝xm，求公园ABCD所占面积S关于x的函数S(x)的解析式；(2)要使公园所占面积最小，休闲区A1B1C1D1的长和宽该如何设计？21．(本题满分12分)已知抛物线y2＝2x，直线l过点(0，2)与抛物线交于M，N两点，以线段MN的长为直径的圆过坐标原点O，求直线l的方程．22．(本题满分12分)已知椭圆的中心在原点，焦点在x轴上，离心率为，且经过点M(4,1)，直线l：y＝x＋m交椭圆于A，B两点．(1)求椭圆的方程；3(2)若直线l不过点M，试问直线MA，MB与x轴能否围成等腰三角形？42014—2015学年度第一学期盟校期末联考高二数学（文科）答案解析一．选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中只有一项是符合题目要求）．题号123456789101112答案CＡBD...