九年级数学第七讲二次函数第一轮复习含答案人教版试卷VIP免费

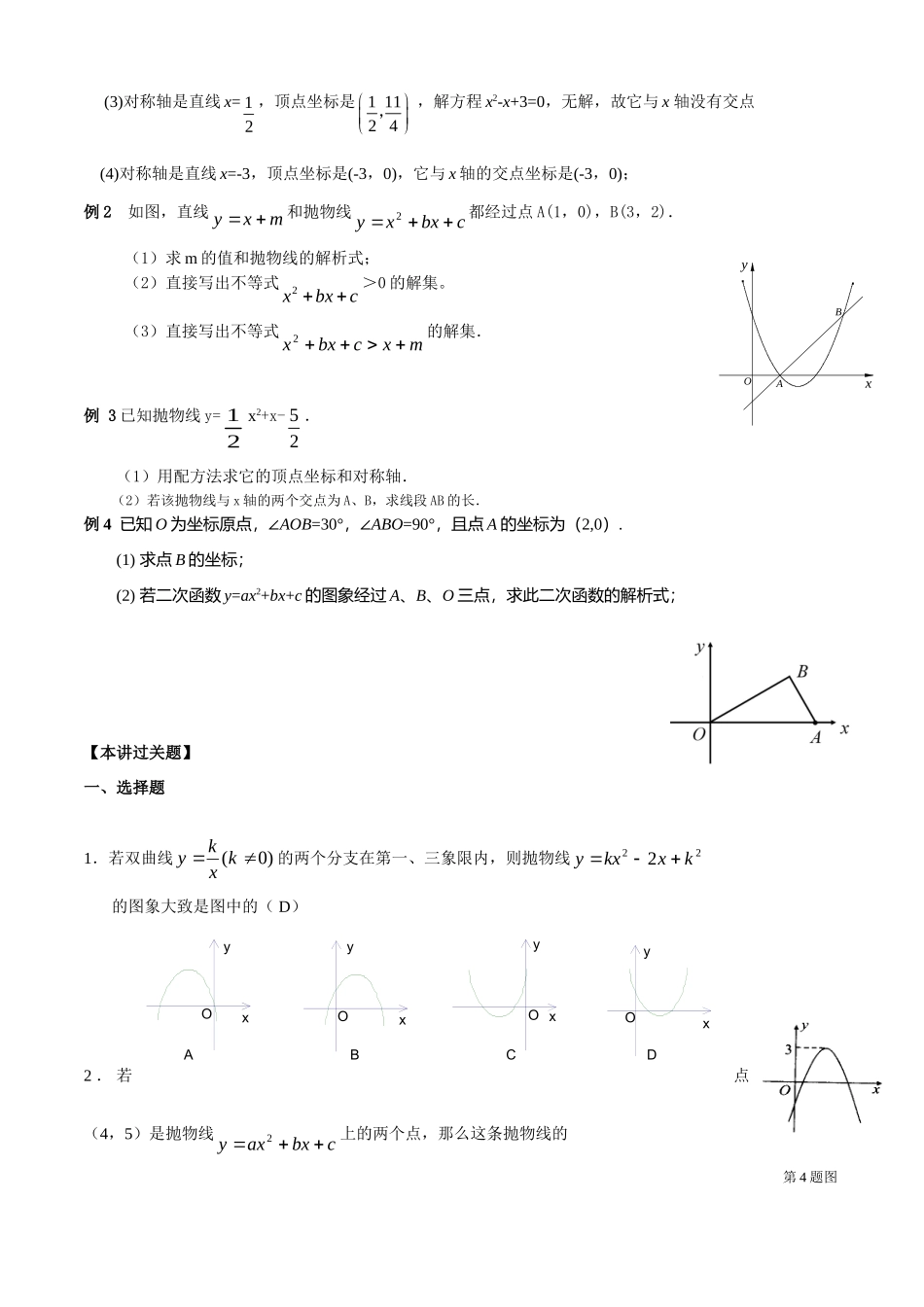
yxO第七讲二次函数学生姓名家长签字【本讲知识要点】1.定义：一般地，形如（是常数，且)0a，叫做二次函数。2.二次函数cbxaxy2用配方法可化成：khxay2的形式，其中h=，k=3.二次函数2()yaxhk的图像和性质a＞0a＜0图象开口对称轴顶点坐标最值当x＝时，y有最值当x＝时，y有最值增减性在对称轴左侧y随x的增大而y随x的增大而在对称轴右侧y随x的增大而y随x的增大而4.抛物线cbxaxy2中，cba,,的作用（1）a决定开口方向及开口大小，如果二次项系数a相同，那么抛物线的开口方向、开口大小完全相同，只是不同.a越大，抛物线张口，a越小，抛物线张口。（2）b和a共同决定抛物线对称轴的位置.由于抛物线cbxaxy2的对称轴是直线abx2，故：①0b时，对称轴为；②0ab（即a、b同号）时，对称轴在y轴侧；③0ab（即a、b异号）时，对称轴在y轴侧.初三数学专题（3）c的大小决定抛物线cbxaxy2与y轴交点的位置.抛物线cbxaxy2与y轴有且只有一个交点。①0c，抛物线经过;②0c,交点在y轴；③0c,交点在y轴。5.用待定系数法求二次函数的解析式（1）一般式：已知图像上三点或三对x、y的值，通常选择一般式.（2）顶点式：已知图像的顶点或对称轴，通常选择顶点式.（3）交点式：已知图像与x轴的交点坐标1x、2x，通常选用交点式：6、2(0)yaxbxca与x轴交点二次函数cbxaxy2的图像与x轴的两个交点的横坐标1x、2x，是对应一元二次方程02cbxax的两个（这也是二次函数与一元二次方程之间的关系）.抛物线与x轴的交点情况可以由对应的一元二次方程的根的判别式判定：①有两个交点（x1，0）和（x2，0）0抛物线与x轴相交；②有一个交点（,0)2ba0抛物线与x轴相切；③没有交点0抛物线与x轴相离.【典型例题】例1．求下列函数的图像的对称轴、顶点坐标及与x轴的交点坐标．(1)y=4x2+24x+35；(2)y=-3x2+6x+2；(3)y=x2-x+3；(4)y=2x2+12x+18．答案：(1)对称轴是直线x=-3，顶点坐标是(-3，-1)，解方程4x2+24x+35=0，得x1=52，x2=72．故它与x轴交点坐标是(52，0)，(72，0)．(2)对称轴是直线x=1，顶点坐标是(1，5)，解方程-3x2+6x+2=0，得1215151;133xx，故它与x轴的交点坐标是．1515(1,0);(1,0)33OyxBA(3)对称轴是直线x=12，顶点坐标是11124，，解方程x2-x+3=0，无解，故它与x轴没有交点(4)对称轴是直线x=-3，顶点坐标是(-3，0)，它与x轴的交点坐标是(-3，0)；例2如图，直线mxy和抛物线cbxxy2都经过点A(1，0)，B(3，2)．（1）求m的值和抛物线的解析式；（2）直接写出不等式2xbxc＞0的解集。（3）直接写出不等式mxcbxx2的解集．例3已知抛物线y=12x2+x-52．（1）用配方法求它的顶点坐标和对称轴．（2）若该抛物线与x轴的两个交点为A、B，求线段AB的长．例4已知O为坐标原点，∠AOB=30°，∠ABO=90°，且点A的坐标为（2,0）.(1)求点B的坐标；(2)若二次函数y=ax2+bx+c的图象经过A、B、O三点，求此二次函数的解析式；【本讲过关题】一、选择题1．若双曲线)0(kxky的两个分支在第一、三象限内，则抛物线222kxkxy的图象大致是图中的（D）2．若点（2，5），（4，5）是抛物线cbxaxy2上的两个点，那么这条抛物线的第4题图xyOxyOxyOOyxDCBA对称轴是（C）A．直线1xB．直线2xC．直线3xD．直线4x3．已知函数772xkxy的图象与x轴有交点，则k的取值范围是（C）A．74kB．047kk且C．47kD．74k且0k4．函数y=ax2+bx+c的图象如图所示，那么关于一元二次方程ax2+bx+c-3=0的根的情况是（C）A．有两个不相等的实数根B．有两个异号的实数根C．有两个相等的实数根D．没有实数根5．已知a<－1，点（a－1，y1），（a，y2），（a+1，y3）都在函数y=x2的图象上，则（C）A．y1