高二数学圆锥曲线综合提高通用版知识精讲VIP免费

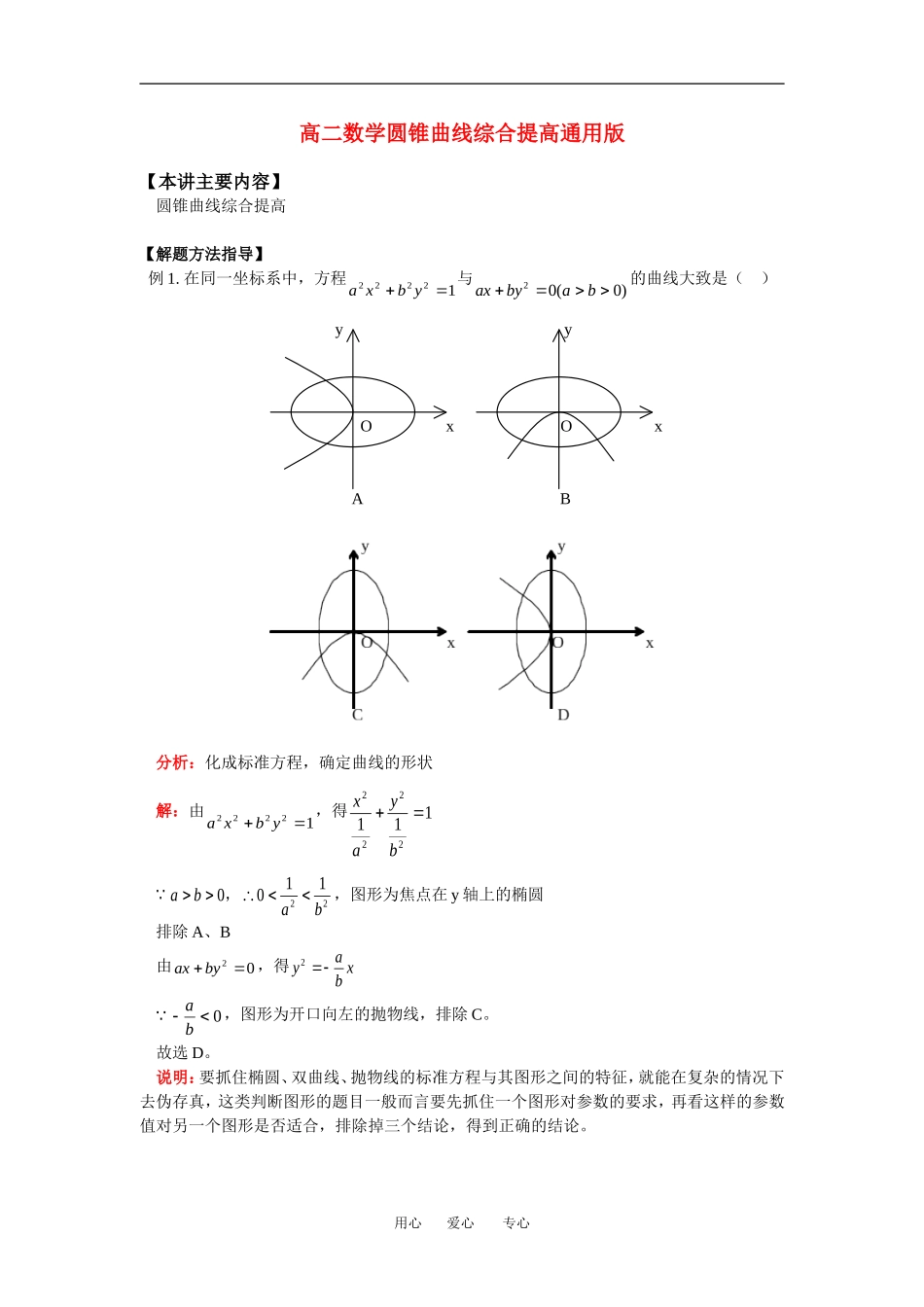
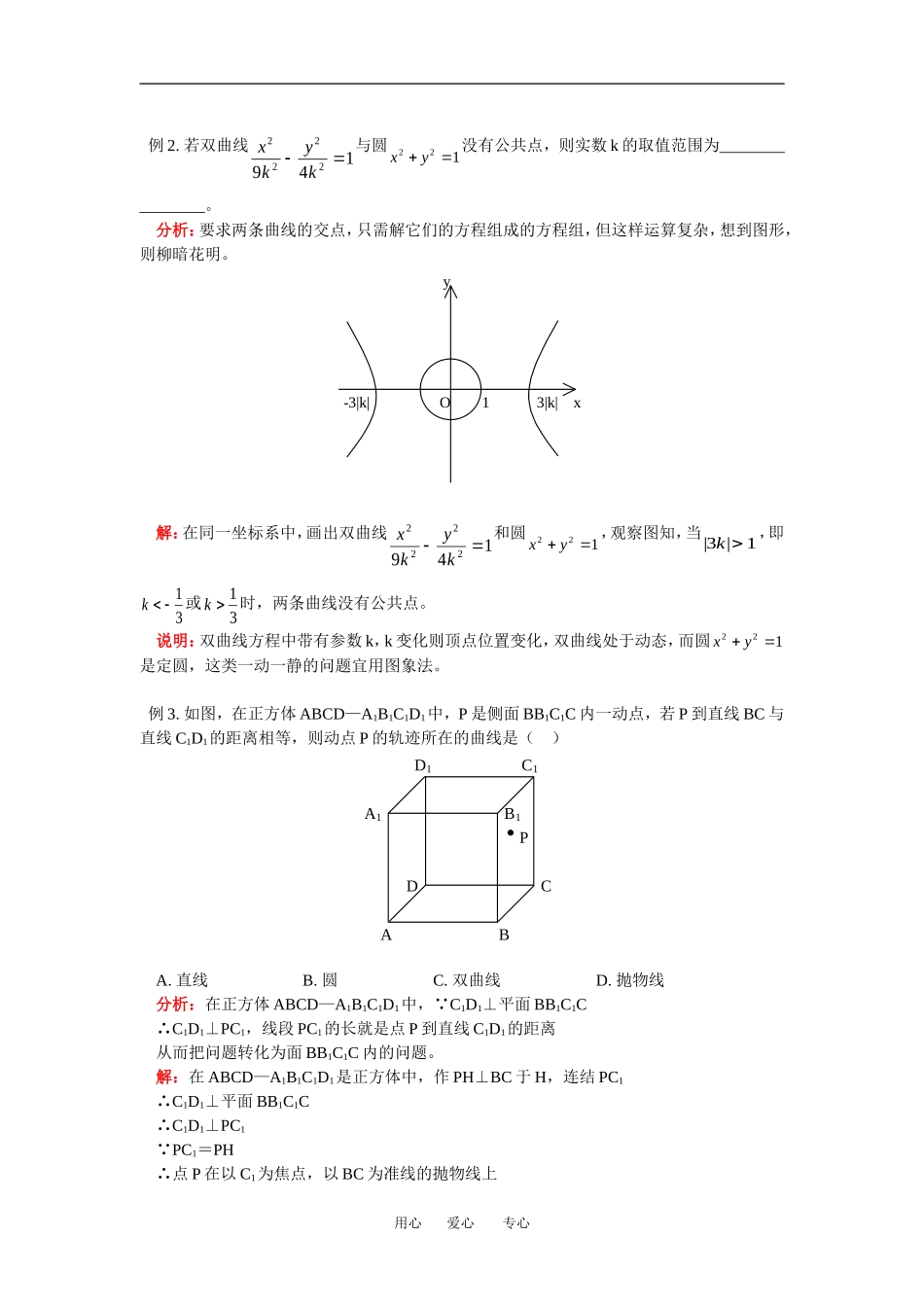
高二数学圆锥曲线综合提高通用版【本讲主要内容】圆锥曲线综合提高【解题方法指导】例1.在同一坐标系中，方程axby22221与axbyab200()的曲线大致是（）yyOxOxAB分析：化成标准方程，确定曲线的形状解：由axby22221，得xayb2222111abab01122，，图形为焦点在y轴上的椭圆排除A、B由axby20，得yabx2ab0，图形为开口向左的抛物线，排除C。故选D。说明：要抓住椭圆、双曲线、抛物线的标准方程与其图形之间的特征，就能在复杂的情况下去伪存真，这类判断图形的题目一般而言要先抓住一个图形对参数的要求，再看这样的参数值对另一个图形是否适合，排除掉三个结论，得到正确的结论。用心爱心专心例2.若双曲线xkyk2222941与圆xy221没有公共点，则实数k的取值范围为________________。分析：要求两条曲线的交点，只需解它们的方程组成的方程组，但这样运算复杂，想到图形，则柳暗花明。y-3|k|O13|k|x解：在同一坐标系中，画出双曲线xkyk2222941和圆xy221，观察图知，当||31k，即k13或k13时，两条曲线没有公共点。说明：双曲线方程中带有参数k，k变化则顶点位置变化，双曲线处于动态，而圆xy221是定圆，这类一动一静的问题宜用图象法。例3.如图，在正方体ABCD—A1B1C1D1中，P是侧面BB1C1C内一动点，若P到直线BC与直线C1D1的距离相等，则动点P的轨迹所在的曲线是（）D1C1A1B1PDCABA.直线B.圆C.双曲线D.抛物线分析：在正方体ABCD—A1B1C1D1中， C1D1⊥平面BB1C1C∴C1D1⊥PC1，线段PC1的长就是点P到直线C1D1的距离从而把问题转化为面BB1C1C内的问题。解：在ABCD—A1B1C1D1是正方体中，作PH⊥BC于H，连结PC1∴C1D1⊥平面BB1C1C∴C1D1⊥PC1 PC1＝PH∴点P在以C1为焦点，以BC为准线的抛物线上用心爱心专心故选D说明：空间问题要向平面作转化，要注意知识的横向联系。例4.求以椭圆的右焦点为焦点，以双曲线的左准线为准线的抛物线方程。分析：先求出椭圆的右焦点和双曲线左准线。解：因为椭圆的右焦点为，双曲线的左准线为。所以所求抛物线的方程为。说明：要牢固掌握圆锥曲线的标准方程及性质。【典型例题分析】例1.（2006年上海春卷）学校科技小组在计算机上模拟航天器变轨返回试验。设计方案如图：航天器运行（按顺时针方向）的轨迹方程为xy22100251，变轨（即航天器运行轨迹由椭圆变为抛物线）后返回的轨迹是以y轴为对称轴、M()0647，为顶点的抛物线的实线部分，降落点为D（8，0）。观测点A（4，0）、B（6，0）同时跟踪航天器。（1）求航天器变轨后的运行轨迹所在的曲线方程；（2）试问：当航天器在x轴上方时，观测点A、B测得离航天器的距离分别为多少时，应向航天器发出变轨指令？yM1O1BDxA分析：（1）应用待定系数法；（2）先求得椭圆与抛物线的变轨点。解：（1）设抛物线的方程为yax2647 降落点D（8，0）在抛物线上用心爱心专心yMC1O1BDxA082472a得a17∴航天器变轨后的运行轨迹所在的曲线方程为：yx176472（2）如图，设变轨点为C（x，y）由方程组xyyx22210025117647消去x2，得473602yy()()4940yyy4，或y94（与y>0相矛盾，舍去）把y＝4代入到yx176472中，得x6或x6（舍去）∴C坐标为（6，4）||||ACBC254，答：当观测点A、B测得离航天器的距离分别为25和4时，应向航天器发出变轨指令。说明：要善于分析，把实际问题转化为所学习的数学问题，用所学数学问题解决实际问题。例2.如图，直线lykxk10：()与直线lykx2：之间的阴影区域（不含边界）记为W，其左半部分记为W1，右半部分记为W2。（I）分别用不等式组表示W1和W2；（II）若区域W中的动点P（x，y）到ll12，的距离之积等于d2，求点P的轨迹C的方程；（III）设不过原点O的直线l与（II）中的曲线C相交于M1，M2两点，且与ll12，分别交于M3，M4两点。求证△OM1M2的重心与△OM3M4的重心重合。用心爱心专心分析：（I）使用试点法即可；（II）按题设去探究；（III）按lx轴，l与x轴不垂直分类讨论。解：（I）Wxykxykxx10{(,)|}，Wxykxykxx20{(,)|}...