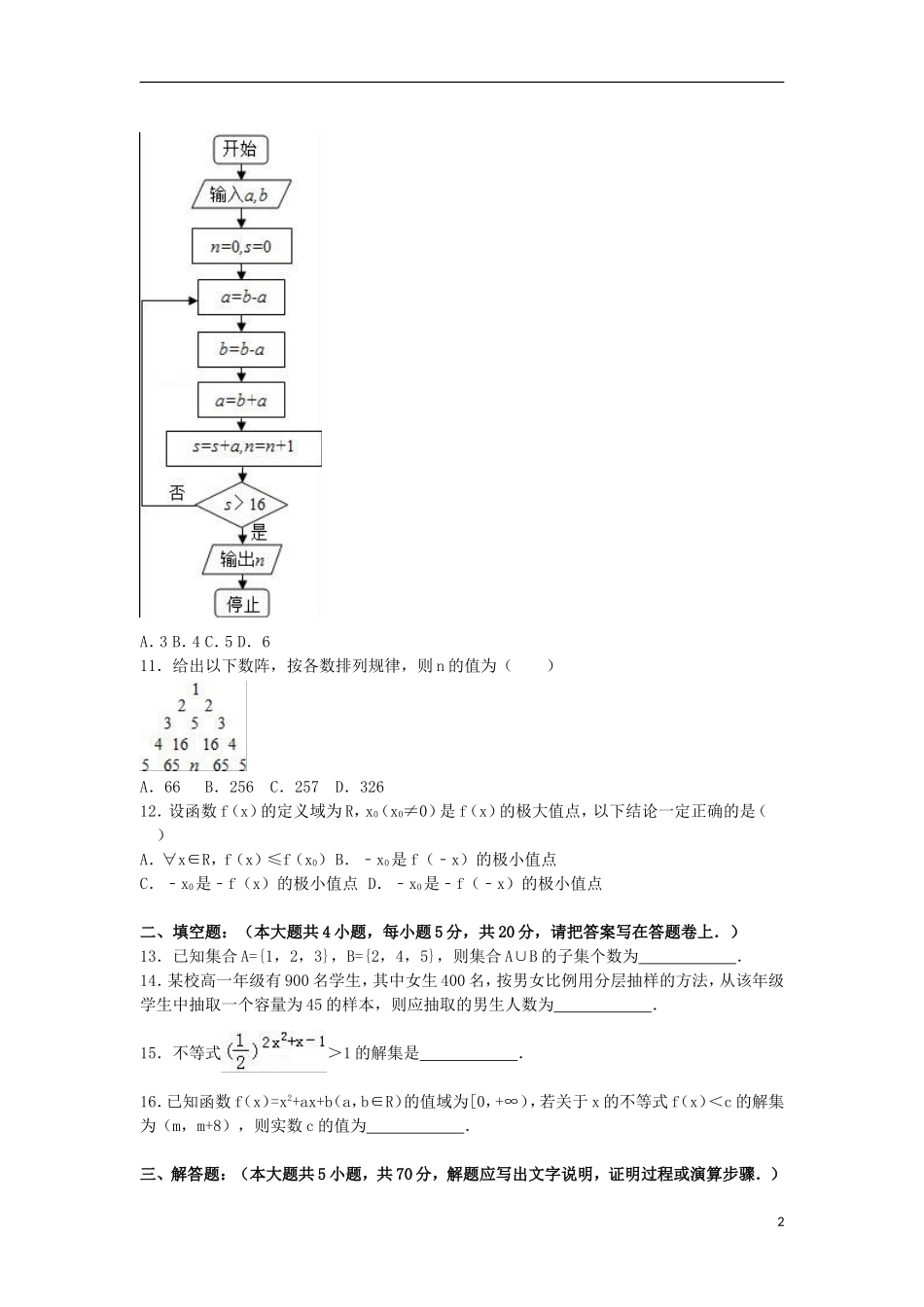
2015-2016学年福建省福州市教院二附中高二(下)期末数学试卷(文科)一.选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的选项中,只有一项是符合题目要求的,把正确答案的序号填入答题卷上的相应空格内.)1.已知集合A={x|2<x<4},B={x|x<3或x>5},则A∩B=()A.{x|2<x<5}B.{x|x<4或x>5}C.{x|2<x<3}D.{x|x<2或x>5}2.设复数z满足z+i=3﹣i,则=()A.﹣1+2iB.1﹣2iC.3+2iD.3﹣2i3.命题“∃x0∈(0,+∞),lnx0=x0﹣1”的否定是()A.∃x0∈(0,+∞),lnx0≠x0﹣1B.∃x0∉(0,+∞),lnx0=x0﹣1C.∀x∈(0,+∞),lnx≠x﹣1D.∀x∉(0,+∞),lnx=x﹣14.已知a,b,c满足c<b<a,且ac<0,下列选项中不一定成立的是()A.ab>acB.c(b﹣a)>0C.ac(a﹣c)<0D.cb2>ab25.重庆市2013年各月的平均气温(℃)数据的茎叶图如,则这组数据的中位数是()A.19B.20C.21.5D.236.设x∈R,则“|x﹣2|<1”是“x2+x﹣2>0”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件7.如果实数x,y满足条件,那么2x﹣y的最大值为()A.﹣1B.﹣2C.2D.18.已知命题p:∀x∈R,sinx+cosx≠2,命题q:∃x0∈R,x02+x0+1<0,则()A.命题p∧(¬q)是真命题B.命题p∧q是真命题C.命题p∨q是假命题D.命题p∨(¬q)是假命题9.若x>0,y>0,且2x+y=2,则的最小值是()A.2B.C.D.10.执行如图程序框图,如果输入的a=4,b=6,那么输出的n=()1A.3B.4C.5D.611.给出以下数阵,按各数排列规律,则n的值为()A.66B.256C.257D.32612.设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是()A.∀x∈R,f(x)≤f(x0)B.﹣x0是f(﹣x)的极小值点C.﹣x0是﹣f(x)的极小值点D.﹣x0是﹣f(﹣x)的极小值点二、填空题:(本大题共4小题,每小题5分,共20分,请把答案写在答题卷上.)13.已知集合A={1,2,3},B={2,4,5},则集合A∪B的子集个数为.14.某校高一年级有900名学生,其中女生400名,按男女比例用分层抽样的方法,从该年级学生中抽取一个容量为45的样本,则应抽取的男生人数为.15.不等式>1的解集是.16.已知函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(m,m+8),则实数c的值为.三、解答题:(本大题共5小题,共70分,解题应写出文字说明,证明过程或演算步骤.)217.已知不等式ax2﹣3x+2>0的解集为{x|x<1或x>b}(1)求a,b的值(2)解不等式ax2﹣(am+b)x+bm<0.18.已知c>0,且c≠1,设p:函数y=cx在R上单调递减;q:函数f(x)=x2﹣2cx+1在(,+∞)上为增函数,若“p且q”为假,“p或q”为真,求实数c的取值范围.19.某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:(1)sin213°+cos217°﹣sin13°cos17°;(2)sin215°+cos215°﹣sin15°cos15°;(3)sin218°+cos212°﹣sin18°cos12°;(4)sin2(﹣18°)+cos248°﹣sin(﹣18°)cos48°;(5)sin2(﹣25°)+cos255°﹣sin(﹣25°)cos55°.(1)试从上述五个式子中选择一个,求出这个常数;(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.20.某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.(1)根据频率分布直方图计算各小长方形的宽度;(2)估计该公司投入4万元广告费之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值)(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:广告投入x(单位:万元)12345销售收益y(单位:万元)2327表格中的数据显示,x与y之间存在线性相关关系,请将(2)的结果填入空白栏,并计算y关于x的回归方程.回归直线的斜率和截距的最小二乘法估计公式分别为=,=﹣.21.已知函数f(x)=(x+1)lnx﹣a(x﹣1).3(I)当a=4时,求曲线y=f(x)在(1,f(1...