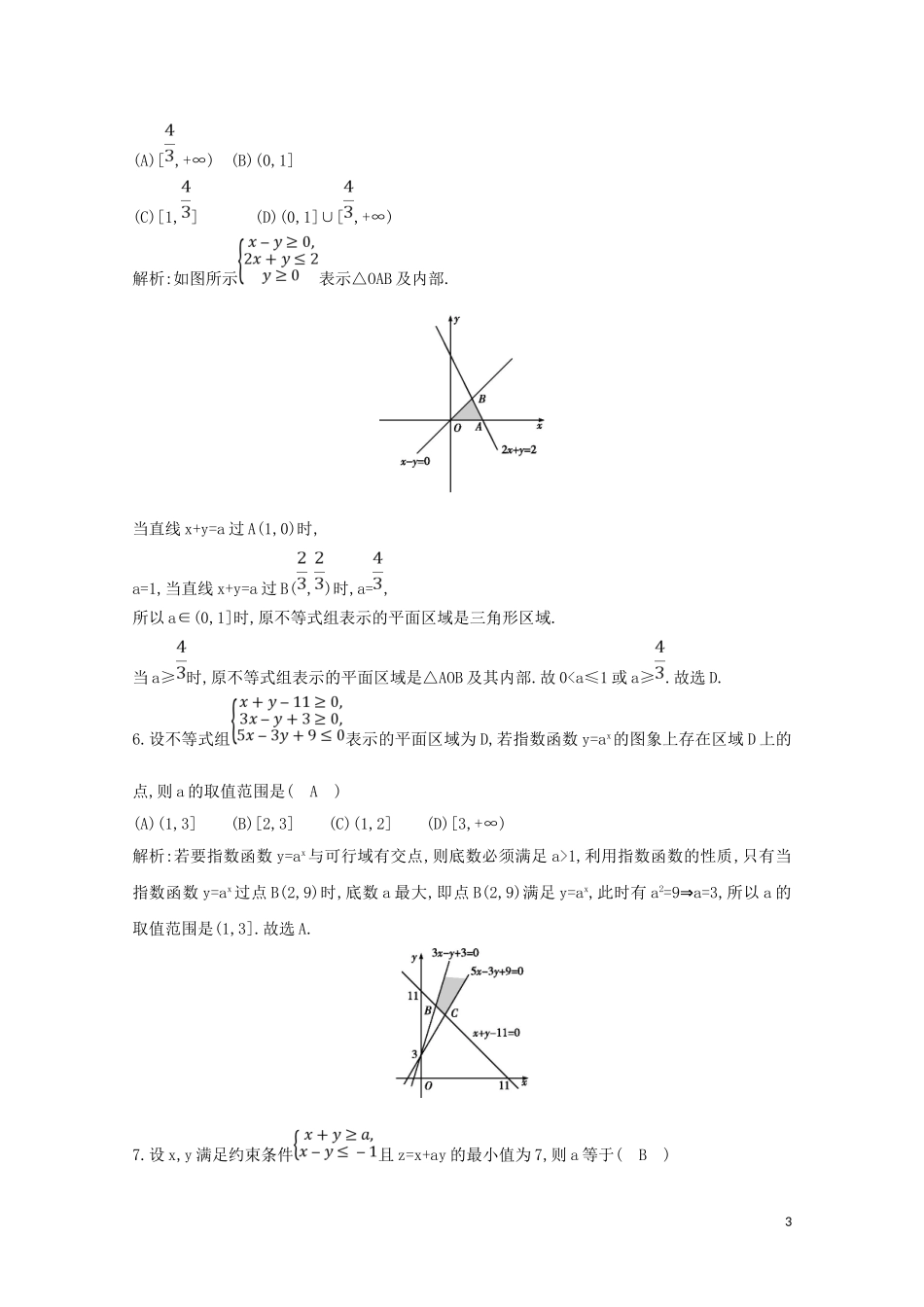
第二课时平面区域与线性规划习题课1.若变量x,y满足约束条件则z=2x-y的最小值等于(A)(A)-(B)-2(C)-(D)2解析:画出可行域,如图阴影部分所示,目标函数变形为y=2x-z,当z最小时,直线y=2x-z的纵截距最大,故将直线y=2x经过可行域,尽可能向上移到过点B(-1,)时,z取到最小值,最小值为z=2×(-1)-=-.故选A.2.设实数x,y满足不等式组则的取值范围是(B)(A)[0,](B)[,](C)[0,](D)[,]解析:不等式组表示的可行域如图阴影部分所示,点A(-3,0)与点(x,y)连线的斜率为,则kAC≤≤kAB,而kAC==,1kAB==.故选B.3.已知实数x,y满足条件若目标函数z=mx-y(m≠0)取得最大值时的最优解有无穷多个,则实数m的值为(A)(A)1(B)(C)-(D)-1解析:作出不等式组表示的平面区域如图阴影部分(包括边界)所示,由图可知当直线y=mx-z(m≠0)与直线2x-2y+1=0重合,即m=1时,目标函数z=mx-y取最大值的最优解有无穷多个,故选A.4.变量x,y满足约束条件若z=2x-y的最大值为2,则实数m等于(C)(A)-2(B)-1(C)1(D)2解析:当m≤时,可行域为开放性区域,z=2x-y无最大值,当m>时不等式组表示区域为三角形OAB,且O(0,0),B(-,).由得A(,),则z=2x-y在A处取得最大值,则-=2,解得m=1,故选C.5.若不等式组表示的平面区域是一个三角形区域,则a的取值范围是(D)2(A)[,+∞)(B)(0,1](C)[1,](D)(0,1]∪[,+∞)解析:如图所示表示△OAB及内部.当直线x+y=a过A(1,0)时,a=1,当直线x+y=a过B(,)时,a=,所以a∈(0,1]时,原不等式组表示的平面区域是三角形区域.当a≥时,原不等式组表示的平面区域是△AOB及其内部.故0
1,利用指数函数的性质,只有当指数函数y=ax过点B(2,9)时,底数a最大,即点B(2,9)满足y=ax,此时有a2=9a=3,⇒所以a的取值范围是(1,3].故选A.7.设x,y满足约束条件且z=x+ay的最小值为7,则a等于(B)3(A)-5(B)3(C)-5或3(D)5或-3解析:画出不等式组对应的平面区域,如图阴影部分所示.联立解得所以A(,).当a=0时A为(-,),z=x+ay的最小值为-,不满足题意;当a<0时,由z=x+ay得y=-x+,要使z最小,则直线y=-x+在y轴上的截距最大,此时最优解不存在;当a>0时,直线过点A时截距最小,z最小,此时z=+=7,解得a=-5(舍去)或a=3.故选B.8.已知O是坐标原点,点A(-1,1),若点M(x,y)为平面区域上的一个动点,则·的取值范围是(C)(A)[-1,0](B)[0,1](C)[0,2](D)[-1,2]解析:作出可行域,如图所示,4·=-x+y.设z=-x+y,作l0:x-y=0,易知,过点(1,1)时,z有最小值,zmin=-1+1=0;过点(0,2)时,z有最大值,zmax=0+2=2,所以·的取值范围是[0,2].故选C.9.若满足条件的点P(x,y)构成三角形区域,则实数k的取值范围是.解析:作出可行域,如图所示.由直线kx-y-2k+1=0得k(x-2)+1-y=0,则直线过定点(2,1).当直线k(x-2)+1-y=0与x+y-2=0平行,即k=-1时,此时对应的平面区域不是三角形,当直线k(x-2)-1-y=0与x-y+2=0平行,即k=1时,对应的平面区域也不是三角形.所以要使对应的平面区域是三角形,则k的取值范围为(-∞,-1)∪(1,+∞).答案:(-∞,-1)∪(1,+∞)10.已知则z=x+y的最大值为.解析:作出可行域,如图中阴影部分所示.5作直线l0:x+y=0,将它向上平移,z=x+y的值也随之增加.当它经过A点时,z取得最大值.解方程组得即A(,).故zmax=+=.答案:11.已知x,y满足约束条件如果(2,)是z=ax-y取得最大值时的最优解,则实数a的取值范围是.解析:画出可行域如图,将目标函数化为直线的斜截式方程y=ax-z,当目标函数的斜率大于等于3y-x=2的斜率时,直线y=ax-z在点(2,)处截距最小,即a≥时,(2,)是目标函数z=ax-y取得最大值时的最优解.答案:[,+∞)12.设变量x,y满足条件则S=5x+4y的最大值是.解析:依据已知条件知不等式组表示的点有(1,1),(1,2),(2,1),(2,2),当x=2,y=2时,Smax=18.6答案:1813.若x,y满足约束条件(1)求目标函数z=x-y+的最值;(2)若目标函数z=ax+2y仅在点(1,0)处取得最小值,求a的取值范围.解:(1)作出可行域如图,可求得A(3,4),B(0,1),C(1,0),平移初始直线y=x,过A(3,4)时z取得最小值-2,过C(1,0)时,z取得最大值1.所以z的最大值为1,最小值为-2.(2)由ax+2y=z,得y=-x+,因为直线ax+2y=z...