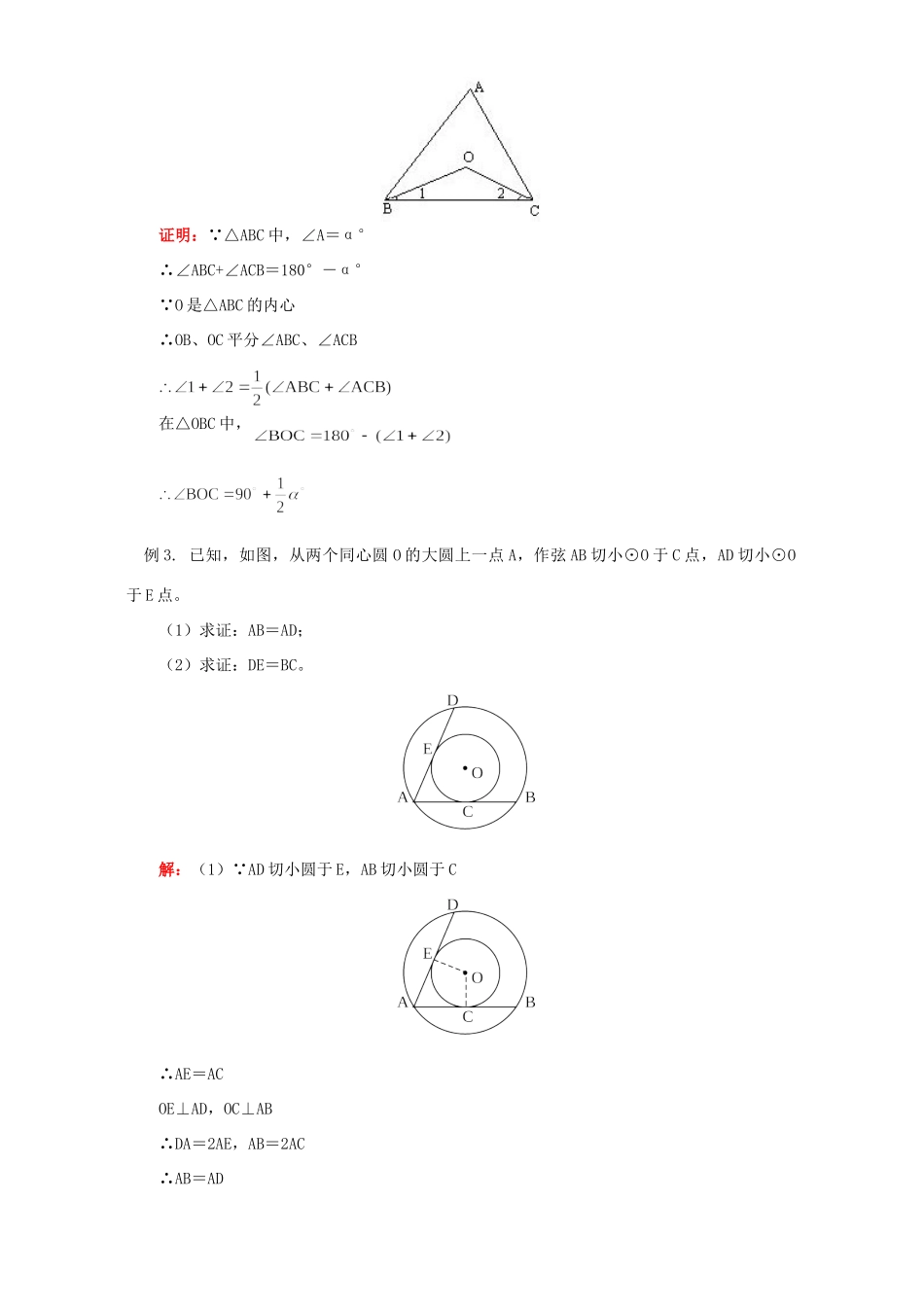
初三数学切线长定理知识精讲【同步教育信息】一.本周教学内容:切线长定理教学目标:1.使学生理解切线长的概念,掌握切线长定理,学会分解和构造“切线长”这个基本图形的技能和技巧。2.培养学生分析总结问题的习惯,提高学生综合运用知识解题的能力,培养数形结合的思想。二.重点、难点:切线长定理是教学重点;切线长定理的灵活运用是教学难点。教学过程:一.知识点1.定义:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。注意:切线和切线长是两个不同的概念,切线是直线,不能度量;切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。2.切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。3.常用辅助线已知PA,PB切⊙O于A,B。(1)(2)(3)(4)图(1)中,有什么结论?(PA=PB)图(2)中,连结AB,增加了什么结论?(增加了∠PAB=∠PBA)图(3)中,再连结OP,增加了什么结论?(增加了∠OPA=∠OPB,OP⊥AB,AC=BC,)。图(4)中,再连结OA,OB。又增加了什么结论?(增加∠OAP=∠OBP=90°,∠AOB+∠APB=180°,以及三角形全等)4.和三角形的各边都相切的圆和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。注意:“接”与“切”是说明三角形顶点和边与圆的关系,顶点都在圆上的叫做“接”,各边都与圆相切的叫做“切”。【典型例题】例1.已知:如图,P为⊙O外一点,PA,PB为⊙O的切线,A和B是切点,BC是直径。求证:AC∥OP。证法一:如下图,连结AB(学生口述,教师板书)证法二:连结AB,交OP于D证法三:连结AB,设OP与交于点E(如上图)PA,PB分别切⊙O于A,B例2.如图,△ABC中,∠A=α°,O是△ABC的内心。求证:证明: △ABC中,∠A=α°∴∠ABC+∠ACB=180°-α° O是△ABC的内心∴OB、OC平分∠ABC、∠ACB在△OBC中,例3.已知,如图,从两个同心圆O的大圆上一点A,作弦AB切小⊙O于C点,AD切小⊙O于E点。(1)求证:AB=AD;(2)求证:DE=BC。解:(1) AD切小圆于E,AB切小圆于C∴AE=ACOE⊥AD,OC⊥AB∴DA=2AE,AB=2AC∴AB=AD(2) AB=AD,AE=AC∴ED=CB例4.已知,如图,PA、PB分别与⊙O相切于A、B点,求证:OP垂直平分线段AB。证明: PA、PB切⊙O于A、B点∴PA=PB∴P在AB的垂直平分线上 OA=OB∴O在AB的垂直平分线上∴PO垂直平分线段AB例5.已知,如图,⊙O是Rt△ABC的内切圆,∠C=90°(1)若AC=12cm,BC=9cm,求⊙O的半径r;(2)若AC=b,BC=a,AB=c,求⊙O的半径r。证明:在Rt△ABC中,AB=15作OD⊥AC,OF⊥BC,OE⊥AB ∠C=90°∴四边形DCFO为矩形 AC、CB切⊙O于D、F∴DC=CF∴四边形DCFO为正方形设半径为r∴DC=CF=r∴AD=12-r,FB=9-r6=2r∴r=3(2)或例6.已知,如图,△ABC的三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r,求:△ABC的面积S。解:连OE、OF、OD 内切圆∴OD⊥AB,OF⊥AC,OE⊥BC例7.已知,如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm,求:BC、AC。证明: AC、BC切⊙O∴∠ACO=∠BCO,∠1=∠2 ∠ACB=90°∴∠ACO=∠BCO=45° ∠BOC=105°∴∠2=30°∴∠ABC=60° AB=20cm,∴BC=10cm例8.已知,如图,⊙O内切于等腰梯形ABCD,切点分别是E、H、F、G,AB//DC,AD=BC(1)求证:线段EF是⊙O的直径;(2)求证:∠AOD=90°;(3)若AB=2a,DC=2b,求此梯形的面积S。证明:(1)法一:连EO并延长交DC于F' DC、AB切⊙O于F、E∴OF⊥DC,OE⊥AB DC//AB,∴DC⊥OF' 过直线外一点有且只有一条直线与已知直线垂直∴F与F'重合∴EF是⊙O的直径法二:共线,连FO,EO∠GOF+∠GDF=180°∠GOE+∠DAE=180° ∠CDA+∠DAE=180°∴∠GOF+∠GOE=180°∴FOE共线(2) DC//AB∴∠CDA+∠DAB=180° OD、AO平分∠CDA、∠DAE∴∠1+∠2=90°∴∠DOA=90°(3)作CC'⊥AB例9.如图,从⊙O外一点A向⊙O引切线AC,从OA上一点B作⊙O的切线BE,切点为E,且BE=AB,求证:AC2=2AO·AB证明:连接OE则OE⊥BE,又OE=OC在Rt△AOC中...