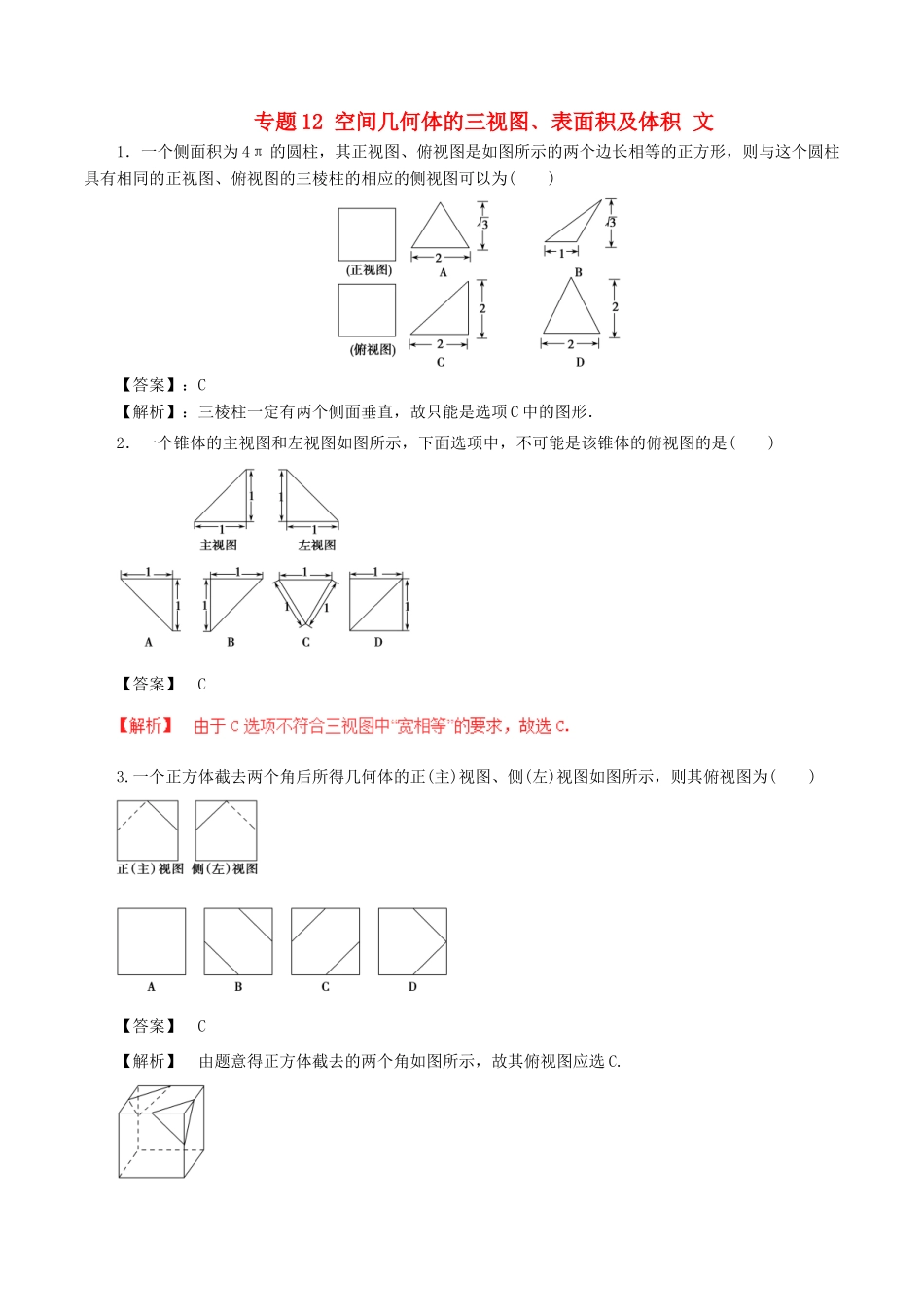
专题12空间几何体的三视图﹑表面积及体积文1.一个侧面积为4π的圆柱,其正视图、俯视图是如图所示的两个边长相等的正方形,则与这个圆柱具有相同的正视图、俯视图的三棱柱的相应的侧视图可以为()【答案】:C【解析】:三棱柱一定有两个侧面垂直,故只能是选项C中的图形.2.一个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是()【答案】C3.一个正方体截去两个角后所得几何体的正(主)视图、侧(左)视图如图所示,则其俯视图为()【答案】C【解析】由题意得正方体截去的两个角如图所示,故其俯视图应选C.4.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为()【答案】C5.如图,用斜二测画法得到四边形ABCD是下底角为45°的等腰梯形,其下底长为5,一腰长为,则原四边形的面积是________.【答案】8【解析】:作DE⊥AB于E,CF⊥AB于F,则AE=BF=ADcos45°=1,∴CD=EF=3.将原图复原(如图),则原四边形应为直角梯形,∠A′=90°,A′B′=5,C′D′=3,A′D′=2,∴S四边形A′B′C′D′=×(5+3)×2=8.6.如图是一个几何体的正视图、侧视图、俯视图,则该几何体的体积是()A.24B.12C.8D.4【答案】B7.某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则其侧视图的面积是()A.B.C.1D.【答案】B【解析】有三视图可以得到原几何体是以1为半径,母线长为2的半个圆锥,故侧视图的面积是,故选B.8.已知某几何体的三视图如图所示,其中,正视图、侧视图均是由三角形与半圆构成的,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为()A.+B.+C.+D.+【答案】C【解析】据三视图可知,该几何体是一个半球(下部)与一个四面体(上部)的组合体,其直观图如图所示,其中BA,BC,BP两两垂直,且BA=BC=BP=1,∴(半)球的直径长为AC=,∴该几何体的体积为V=V半球+VPABC=×π+××BA·BC·PB=+.9.某个几何体的三视图如图所示(其中正视图中的圆弧是半径为2的半圆),则该几何体的表面积为()A.92+24πB.82+24πC.92+14πD.82+14π【答案】C10.四棱锥PABCD的三视图如图所示,四棱锥PABCD的五个顶点都在一个球面上,E,F分别是棱AB,CD的中点,直线EF被球面所截得的线段长为2,则该球的表面积为()A.12πB.24πC.36πD.48π【答案】A11.用6根木棒围成一个棱锥,已知其中有两根的长度为cm和cm,其余四根的长度均为1cm,则这样的三棱锥的体积为________cm3.【答案】【解析】由题意知该几何体如图所示,SA=SB=SC=BC=1,AB=,AC=,则∠ABC=90°,取AC的中点O,连接SO、OB,则SO⊥AC,所以SO==,OB=AC=,又SB=1,所以SO2+OB2=SB2,所以∠SOB=90°,又SO⊥AC,所以SO⊥底面ABC,故所求三棱锥的体积V=××=.12.如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为________.【答案】24【解析】由题意知原图形OABC是平行四边形,且OA=BC=6,设平行四边形OABC的高为OE,则OE××=O′C′, O′C′=2,∴OE=4,∴S▱OABC=6×4=24.13.如图所示,E,F分别是正方体的面ADD1A1,面BCC1B1的中心,则四边形BFD1E在该正方体的面上的正投影可能是________.(要求:把可能的图的序号都填上)【答案】②③【解析】由正投影的定义,四边形BFD1E在面AA1D1D与面BB1C1C上的正投影是图③;其在面ABB1A1与面DCC1D1上的正投影是图②;其在面ABCD与面A1B1C1D1上的正投影也是②,故①④错误.14.用一个平行于圆锥底面的平面截这个圆锥,截得圆台的上、下底面的面积之比为1∶16,截去的圆锥的母线长是3cm,求圆台的母线长.15.如图是一个几何体的正视图和俯视图.(1)试判断该几何体是什么几何体;(2)画出其侧视图,并求该平面图形的面积;(3)求出该几何体的体积.16.已知某几何体的俯视图是如右图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V;(2)求该几何体的侧面积S.【解析】由题设可知,几何体是一个高为4的四...