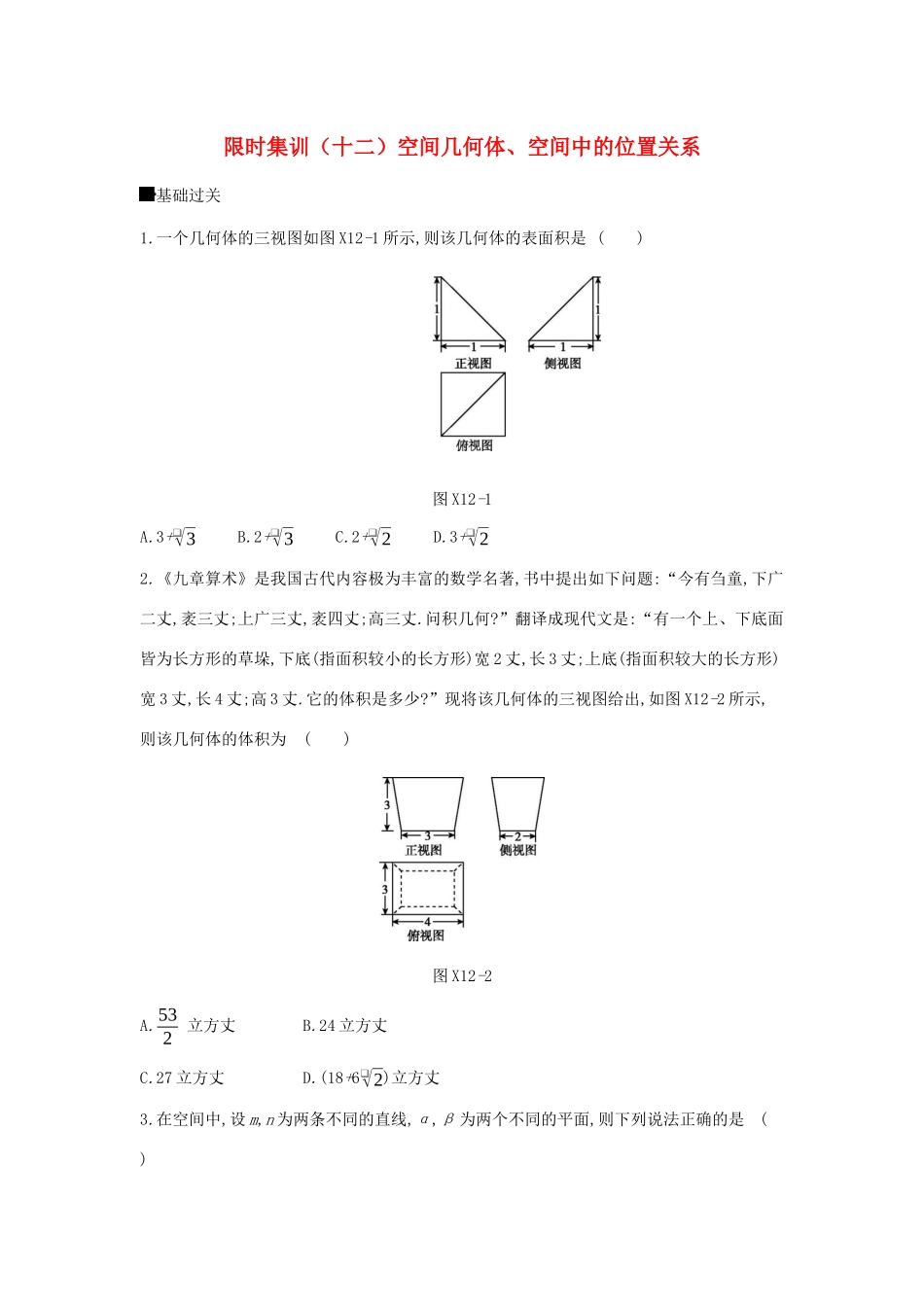
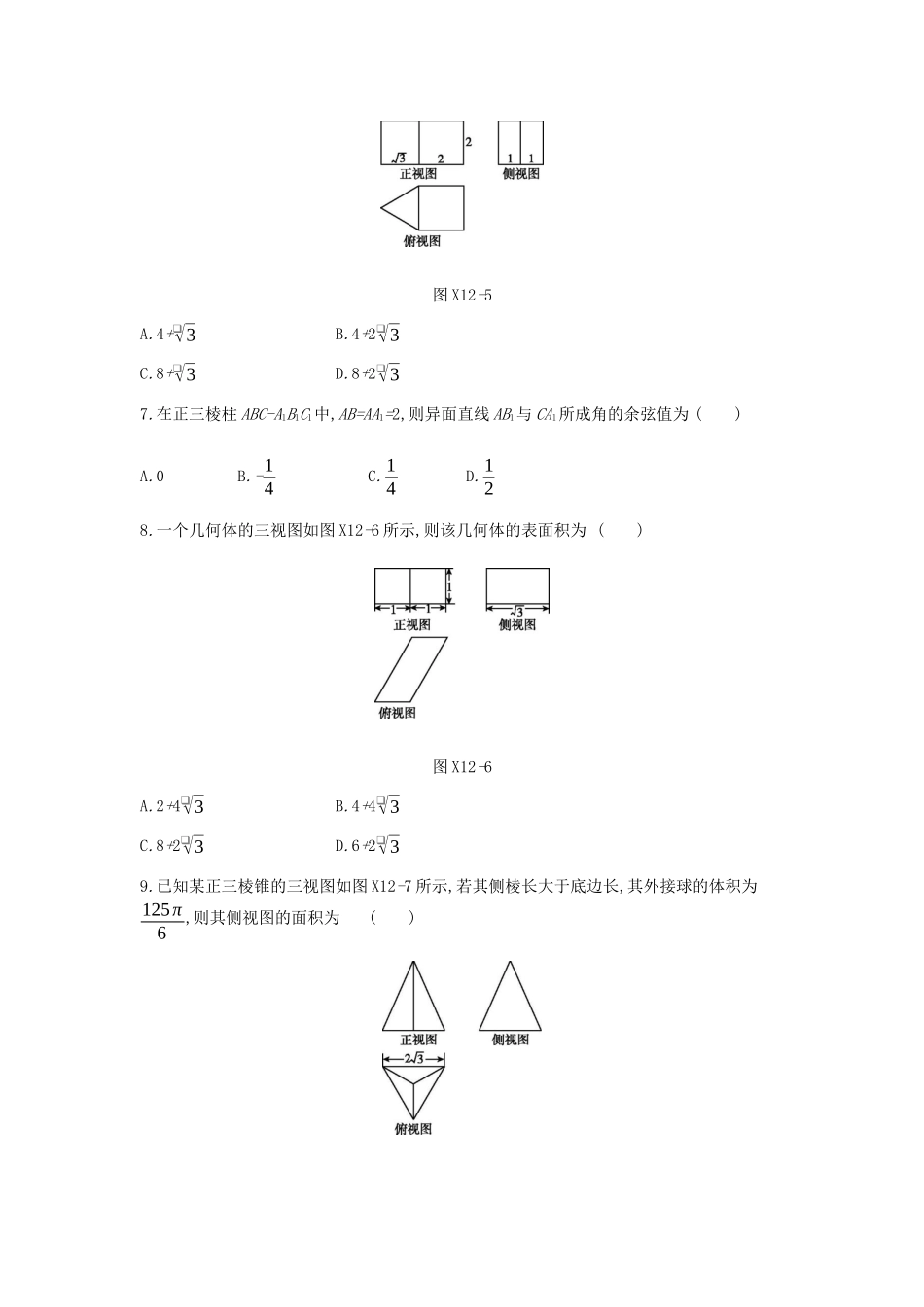
限时集训(十二)空间几何体、空间中的位置关系基础过关1.一个几何体的三视图如图X12-1所示,则该几何体的表面积是()图X12-1A.3+❑√3B.2+❑√3C.2+❑√2D.3+❑√22.《九章算术》是我国古代内容极为丰富的数学名著,书中提出如下问题:“今有刍童,下广二丈,袤三丈;上广三丈,袤四丈;高三丈.问积几何?”翻译成现代文是:“有一个上、下底面皆为长方形的草垛,下底(指面积较小的长方形)宽2丈,长3丈;上底(指面积较大的长方形)宽3丈,长4丈;高3丈.它的体积是多少?”现将该几何体的三视图给出,如图X12-2所示,则该几何体的体积为()图X12-2A.532立方丈B.24立方丈C.27立方丈D.(18+6❑√2)立方丈3.在空间中,设m,n为两条不同的直线,α,β为两个不同的平面,则下列说法正确的是()A.若m∥α且α∥β,则m∥βB.若α⊥β,m⊂α,n⊂β,则m⊥nC.若m⊥α且α∥β,则m⊥βD.若m不垂直于α,且n⊂α,则m必不垂直于n4.如图X12-3所示,平面α与平面β相交于BC,AB⊂α,CD⊂β,点A∉BC,点D∉BC,则下列说法错误的是()图X12-3A.直线AD与BC是异面直线B.过AD只能作一个平面与BC平行C.过AD总能作一个平面与BC垂直D.过点D只能作一个平面与BC垂直,但过点D可作无数个平面与BC平行5.一个几何体的三视图如图X12-4所示,若该几何体的体积为323,则该几何体的外接球的表面积为()图X12-4A.12πB.24πC.36πD.48π6.某几何体的三视图如图X12-5所示,则该几何体的体积为()图X12-5A.4+❑√3B.4+2❑√3C.8+❑√3D.8+2❑√37.在正三棱柱ABC-A1B1C1中,AB=AA1=2,则异面直线AB1与CA1所成角的余弦值为()A.0B.-14C.14D.128.一个几何体的三视图如图X12-6所示,则该几何体的表面积为()图X12-6A.2+4❑√3B.4+4❑√3C.8+2❑√3D.6+2❑√39.已知某正三棱锥的三视图如图X12-7所示,若其侧棱长大于底边长,其外接球的体积为125π6,则其侧视图的面积为()图X12-7A.32B.2C.4D.610.已知四棱锥P-ABCD的侧棱长都相等,且底面是边长为3❑√2的正方形,若它的五个顶点都在直径为10的球面上,则四棱锥P-ABCD的体积为.11.如图X12-8所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点,则异面直线AE与BD1所成角的余弦值为.图X12-8能力提升12.已知某四棱锥的三视图如图X12-9所示,则该四棱锥的五个面中,面积最大的面的面积是()图X12-9A.3B.6C.8D.1013.如图X12-10所示,α∩β=l,点A,C∈α,点B,D∈β,且A,B,C,D∉l,点M,N分别是线段AB,CD的中点,则下列说法中正确的是()图X12-10A.当CD=2AB时,M,N不可能重合B.M,N可能重合,但此时直线AC与l不可能相交C.当直线AB,CD相交,且AC∥l时,直线BD与l不可能平行D.当直线AB,CD异面时,直线MN与l可能平行14.已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧棱PA⊥平面ABCD,PA=2,若在四棱锥P-ABCD的内部有一个半径为R的球,则R的最大值为()A.2-❑√2B.1C.❑√2-1D.2❑√315.一个正三棱柱的三视图如图X12-11所示,若该三棱柱的外接球的表面积为32π,则侧视图中的x的值为()图X12-11A.6B.4C.3D.216.某几何体的正视图和俯视图如图X12-12所示,在如图X12-13所示的图形中,可能是该几何体侧视图的是.(写出所有可能的图形的序号)图X12-12图X12-1317.若直三棱柱ABC-A1B1C1的各个顶点都在同一个球面上,且AB=3,AC=5,BC=7,AA1=2,则此球的表面积等于.18.如图X12-14①所示,在矩形ABCD中,AB=2,BC=1,E是DC的中点,现将△DAE沿AE折起,使得平面DAE⊥平面ABCE,得到如图X12-14②所示的几何体,则异面直线AE和DB所成角的余弦值为.图X12-14限时集训(十二)基础过关1.C[解析]由三视图可得该几何体是一个四棱锥,其底面是边长为1的正方形,故底面积为1,侧面均为直角三角形,其中有两个是腰长为1的等腰直角三角形,面积均为12,另外两个是边长分别为1,❑√2,❑√3的直角三角形,面积均为❑√22,故该几何体的表面积S=1+2×12+2×❑√22=2+❑√2.故选C.2.A[解析]将该几何体下底面的4个顶点正投影在上底面,将几何体分割,中间为一个长方体,其体积为2×3×3=18(立方丈),剩余的部分可以分割为4个四棱锥和4个三棱柱,剩余部分的体积为4×13×12×12×3+2×12×12×3×2+2×12×12×3×3=172(立方丈),所以该几何体的体积为532立方丈.3.C[解析]对于A,若m∥α且α∥β,也有m⊂β的可能,故A中说法错误;...