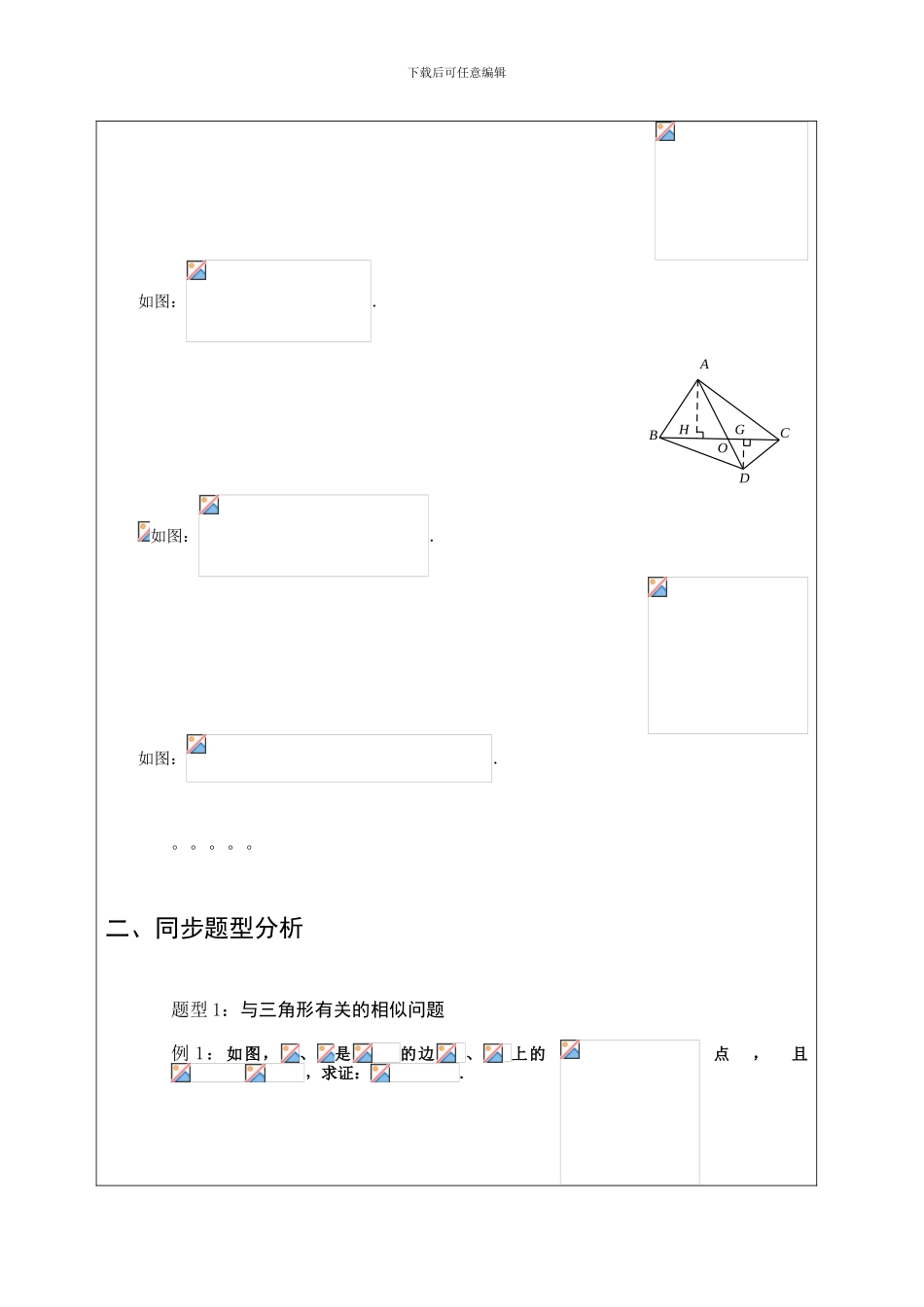
下载后可任意编辑相似三角形一、同步知识梳理知识点1:相似证明中的基本模型IHGFEDCBAGFEDCBAEDCBAEDCBAEFDCBAFEDCBAODCBAODCBAHEDCBAEDCBAEDCBAODCBADCBDBACAEDCBADCBAGFEDCBAGFEDCBAGFEDCBADEFCBA下载后可任意编辑HPMNFEDCBAGHGFEDCBAEFDCBAFEDCBA知识点2:相似证明中常见辅助线的作法在相似的证明中,常见的辅助线的作法是做平行线构造成比例线段或相似三角形,同时再结合等量代换得到要证明的结论.常见的等量代换包括等线代换、等比代换、等积代换等.如图:平分交于,求证:.321EDCAB证法一:过作,交的延长线于.∴,. ,∴.∴. ,∴.点评:做平行线构造成比例线段,利用了“A”型图的基本模型.证法二;过作的平行线,交的延长线于.∴,∴. ,∴.点评:做平行线构造成比例线段,利用了“X”型图的基本模型.知识点3:相似证明中的面积法面积法主要是将面积的比,和线段的比进行相互转化来解决问题.常用的面积法基本模型如下:下载后可任意编辑如图:.GHODCBA如图:.如图:.。。。。。二、同步题型分析题型1:与三角形有关的相似问题例1:如图,、是的边、上的点,且,求证:.下载后可任意编辑解析:例2:如图,在中,于,于,的面积是面积的4倍,,求的长.解析:题型2:相似中的角平分线问题例1:如图,是的角平分线,求证:解析:例2:已知中,的外角平分线交对边的延长线于,求证:解析:下载后可任意编辑例3:已知:、分别为的内、外角平分线,为的中点,求证:解析:题型3:型结论的证明例1:如图,直角中,,,证明:,,.解析:下载后可任意编辑例2:如图,在中,平分,的垂直平分线交于,交的延长线于,求证:.解析:题型4、三角形内接矩形问题例1、已知,如图,中,,四边形为正方形,其中在边上,在上,求正方形的边长.解析:下载后可任意编辑三、课堂达标检测检测题1:如图,在正方形ABCD中,点E在AB边上,且AE∶EB=2∶1,AF⊥DE于G交BC于F,则△AEG的面积与四边形BEGF的面积之比为()A、1∶2B、1∶4C、4∶9D、2∶3检测题2、如图,已知DE∥BC,CD和BE相交于点O,∶=4∶9,则AE∶EC为()A、2∶1B、2∶3C、4∶9D、5∶4检测题3、在△ABC中,D为AC边上一点,∠DBC=∠A,BC=,AC=3,则CD的长为()A、1B、C、2D、答案:1、C2、A3、C下载后可任意编辑一、专题精讲构造相似辅助线——双垂直模型例1:在△ABC中,AB=,AC=4,BC=2,以AB为边在C点的异侧作△ABD,使△ABD为等腰直角三角形,求线段CD的长.答案:解:情形一:下载后可任意编辑情形二:情形三:例2:在△ABC中,AC=BC,∠ACB=90°,点M是AC上的一点,点N是BC上的一点,沿着直线MN折叠,使得点C恰好落在边AB上的P点.求证:MC:NC=AP:PB.下载后可任意编辑答案:证明:方法一:连接PC,过点P作PD⊥AC于D,则PD//BC根据折叠可知MN⊥CP2+ ∠∠PCN=90°,∠PCN+∠CNM=90°2=∴∠∠CNM ∠CDP=∠NCM=90°∴△PDC∽MCN∴MC:CN=PD:DC PD=DA∴MC:CN=DA:DC PD//BC∴DA:DC=PA:PB∴MC:CN=PA:PB方法二:如图,过M作MD⊥AB于D,过N作NE⊥AB于E由双垂直模型,可以推知△PMD∽NPE,则,根据等比性质可知,而MD=DA,NE=EB,PM=CM,PN=CN,∴MC:CN=PA:PB例3:已知,如图,直线y=2﹣x+2与坐标轴交于A、B两点.以AB为短边在第一象限做一个矩形ABCD,使得矩形的两边之比为12﹕。求C、D两点的坐标。下载后可任意编辑构造相似辅助线——A、X字型例4:如图:△ABC中,D是AB上一点,AD=AC,BC边上的中线AE交CD于F。求证:答案:证明:(方法一)如图延长AE到M使得EM=AE,连接CM BE=CE,∠AEB=∠MEC∴△BEA≌△CEM∴CM=AB,∠1=∠B∴AB∥CM∴∠M=∠MAD,∠MCF=∠ADF∴△MCF∽△ADF∴ CM=AB,AD=AC∴下载后可任意编辑(方法二)过D作DG∥BC交AE于G则△ABE∽△ADG,△CEF∽△DGF∴, AD=AC,BE=CE∴例5:四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB。求证:答案:证明:过点D作DF∥AB交AC的延长线于点F,则∠2=3∠ AC平分∠DAB下载后可任意编辑1=2∴∠∠1=3∴∠∠∴AD=DF ∠DEF=∠BEA,∠2=3∠∴△BEA∽△DEF∴ AD=DF∴ AC为AB、AD的比例中项∴即又 ∠1=2∠∴△ACD∽△ABC∴∴∴...