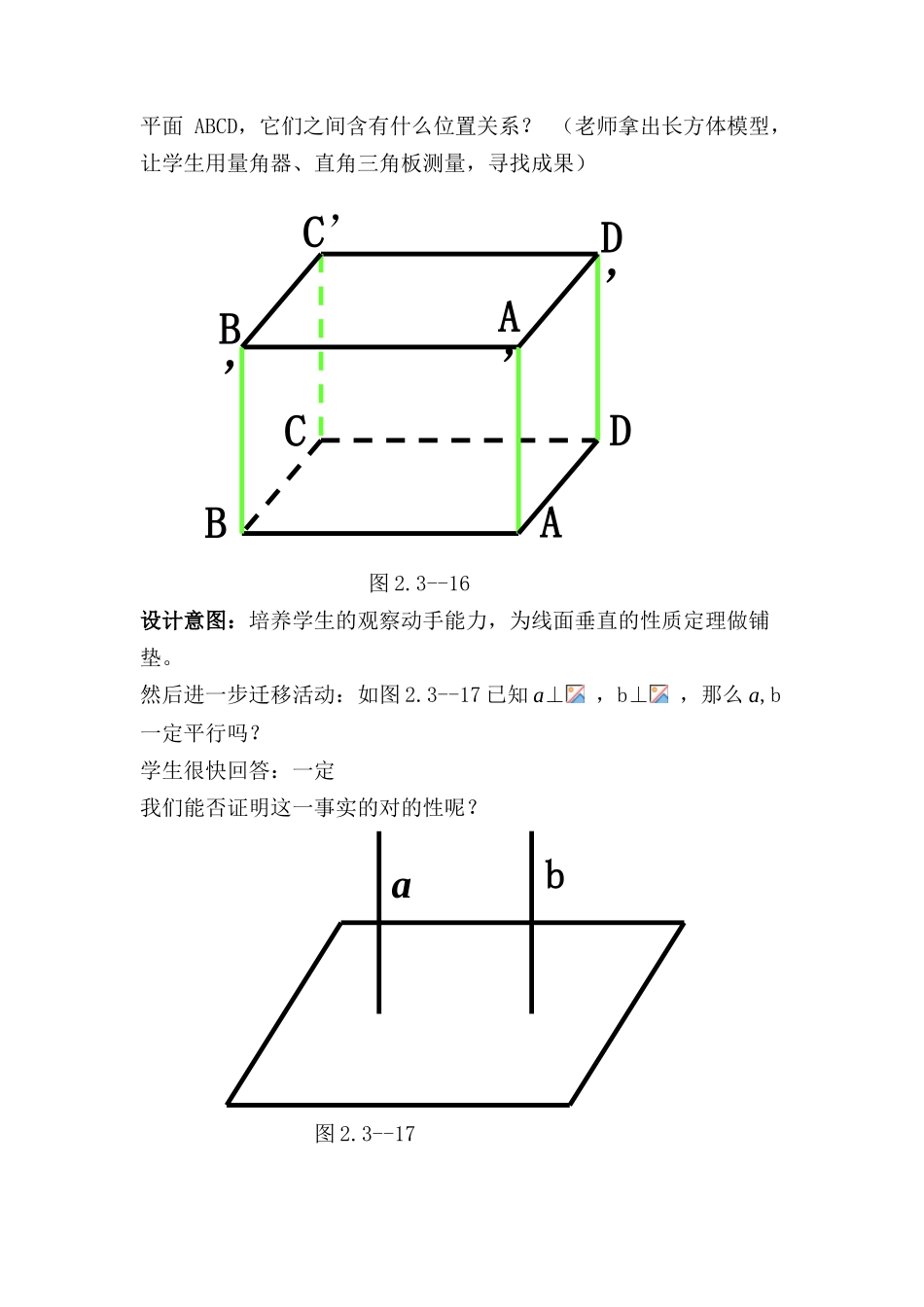
2.3.3直线与平面垂直的性质教学设计课标规定:以立体几何的定义、公理、定理为出发点,通过直观感知、操作确认,归纳出直线与平面垂直的性质定理,并加以证明。学情分析:在学习本节课的内容之前,刚刚学习了直线与平面垂直的定义以及鉴定定理,在学完鉴定定理之后紧接着的例1当中我们运用鉴定定理证明了线线平行的性质定理,即如果两条平行直线中的一条垂直于一种平面,那么另一条也垂直于同一种平面,用符号语言表达为若a//b,a⊥α,则b⊥α。而我们的直线与平面垂直的性质定理就是将上述命题的中的题设和结论变化一下得到的。因此在前面知识的基础上学习本节课的内容并不是很难。教材分析:1.本节的作用和地位:本节课是人教版必修2第二章直线与平面垂直的第三学时。空间中直线与平面之间的位置关系中,垂直是一种非常重要的位置关系,它不仅应用较多,并且是空间问题平面化的典范。空间中直线与平面垂直的性质定理不仅是由线面关系转化为线线关系,并且将垂直关系转化为平行关系,因此直线与平面垂直的性质定理在立体几何中有着重要的地位和作用。2.本节重要内容:直线与平面垂直的性质定理的证明及转化思想的渗入。教学目的:1.知识与技能:掌握直线与平面垂直的性质定理,理解线面关系与线线关系,垂直关系与平行关系之间的转化以及反证法的应用。2.过程与办法:在观察长方体模型的基础上进行操作确认,获得对性质定理对的性的认识,进一步推导出定理的证明过程。3.情感态度与价值观:通过“直观感知、操作确认,推理证明”,提高空间想象的能力和逻辑推理能力。教学重点:直线与平面垂直的性质定理的证明及转化思想的渗入。教学难点:直线与平面垂直的性质定理的证明教学理念:高中学生思维活跃,参加意识、自主探究能力较强,整节课重要以学生自主探究为主,老师只起一种组织,引导的作用。从而增强空间想象能力,养成质疑思辨、创新的精神。教学办法:探究讨论法教学用品:长方体模型,量角器,直角三角板,多媒体教学设计:一.创设情境,揭示课题问题:(实物式引入):(1)两根旗杆垂直于地面,给我们以旗杆平行的形象(2)让学生双手各持一支笔直立与桌面,通过操作确认两支笔平行。数学来源于生活,把这些问题抽象概括得到一种新的问题:若a⊥,b⊥,那a和b会有如何的位置关系呢?让学生自由讲话,教师不急于下结论,而是继续引导学生:欲知结论如何,让我们一起来观察、探讨。(自然进入课题内容)设计意图:现实生活中的问题更能激发学生的学习爱好,让学生从现实生活中发现数学,将问题化归为数学问题,感受数学来源于生活,又服务于生活。二.猜想推测,激发爱好1、操作确认观察长方体模型中四条侧棱与同一种底面的位置关系。先来看书上70页的思考题:如图2.3-16,长方体ABCD-A’B’C’C’中,棱AA’,BB’,CC’,DD’所在直线都垂直于平面ABCD,它们之间含有什么位置关系?(老师拿出长方体模型,让学生用量角器、直角三角板测量,寻找成果)图2.3--16设计意图:培养学生的观察动手能力,为线面垂直的性质定理做铺垫。然后进一步迁移活动:如图2.3--17已知a⊥,b⊥,那么a,b一定平行吗?学生很快回答:一定我们能否证明这一事实的对的性呢?图2.3--17AA’CDB’C’D’abB设计意图:借助长方体模型让学生感知直线与平面的垂直关系,使学生学会从“感性认识”到“理性认识”过程中获取新知。2、推理证明教师提问:如何用数学语言证明这个猜想是对的的。(给时间学生思考,已知是什么,结论是什么,如何由条件证明结论)抽查学生证明过程:如图所示教师追问:证明过程有问题吗?有学生回答:直线a,b不一定共面。教师:由已知a⊥,b⊥,直接证明结论a//b很困难,怎么办?三.层层推动,推理证明教师启发学生:1、怎么想到用反证法证明①证明两条a,b平行有哪些办法呢?初中有哪些?(同位角相等、内错角相等、同旁内角互补、中位线定理、平行四边形性质等)高中哪些?(公理4)这些办法对本题证明有用吗?②空间两直线a,b的位置关系有哪些?(平行、异面、相交)③空间垂直于同一条直线的两直线一定平行吗?(平行、异面、相交)abAB教师追问:只要能证明异面、相...