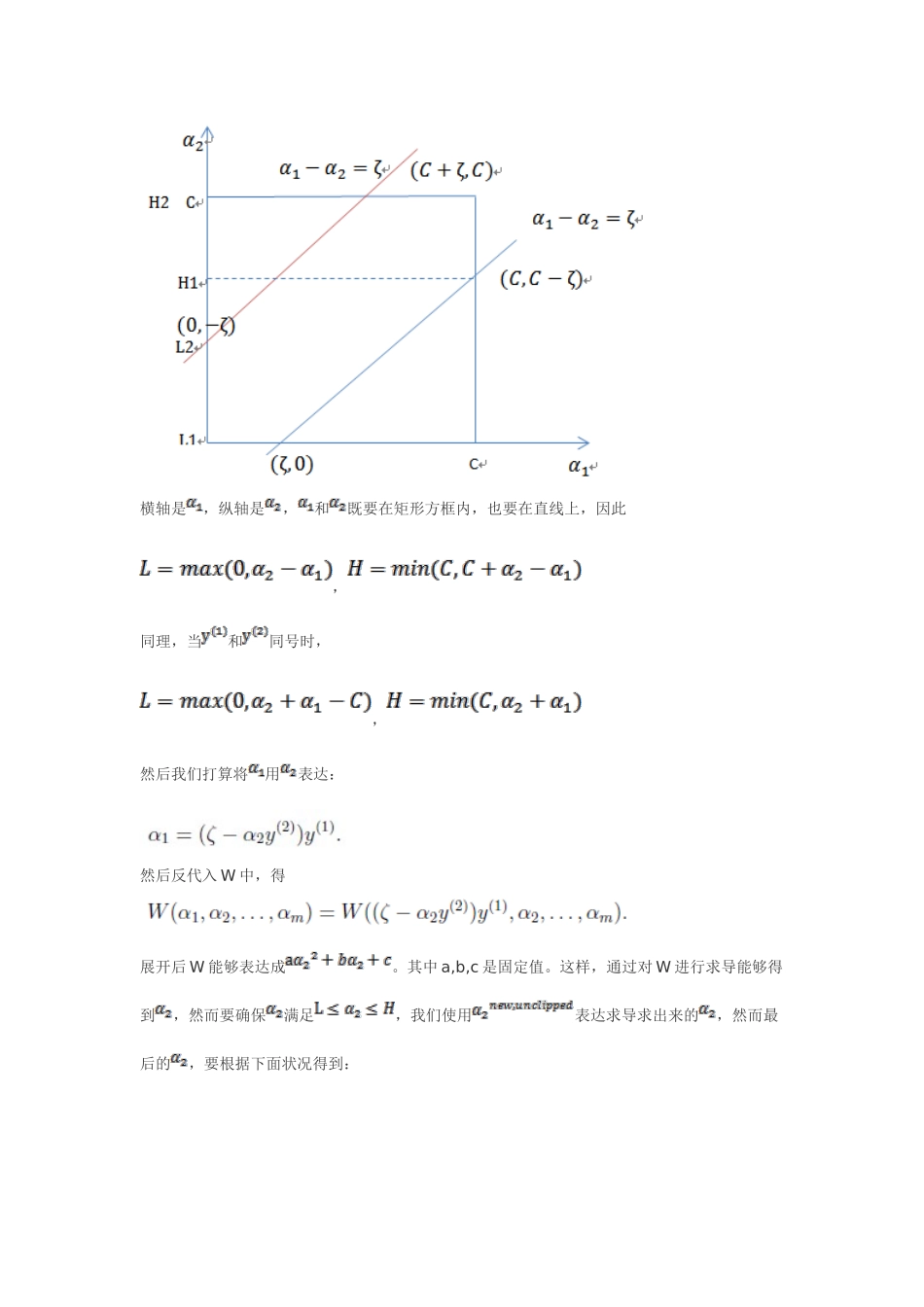
支持向量机(五)SMO算法11SMO优化算法(Sequentialminimaloptimization)SMO算法由MicrosoftResearch的JohnC.Platt在1998年提出,并成为最快的二次规划优化算法,特别针对线性SVM和数据稀疏时性能更优。有关SMO最佳的资料就是他本人写的《SequentialMinimalOptimizationAFastAlgorithmforTrainingSupportVectorMachines》了。我拜读了一下,下面先说讲义上对此办法的总结。首先回到我们前面始终悬而未解的问题,对偶函数最后的优化问题:要解决的是在参数上求最大值W的问题,至于和都是已知数。C由我们预先设定,也是已知数。按照坐标上升的思路,我们首先固定除以外的全部参数,然后在上求极值。等一下,这个思路有问题,由于如果固定以外的全部参数,那么将不再是变量(能够由其它值推出),由于问题中规定了因此,我们需要一次选用两个参数做优化,例如和,此时能够由和其它参数表达出来。这样回带到W中,W就只是有关的函数了,可解。这样,SMO的重要环节以下:意思是,第一步选用一对和,选用办法使用启发式办法(背面讲)。第二步,固定除和之外的其它参数,拟定W极值条件下的,由表达。SMO之因此高效就是由于在固定其它参数后,对一种参数优化过程很高效。下面讨论具体办法:假设我们选用了初始值满足了问题中的约束条件。接下来,我们固定,这样W就是和的函数。并且和满足条件:由于都是已知固定值,因此为了方面,可将等式右边标记成实数值。当和异号时,也就是一种为1,一种为-1时,他们能够表达成一条直线,斜率为1。以下图:横轴是,纵轴是,和既要在矩形方框内,也要在直线上,因此,同理,当和同号时,,然后我们打算将用表达:然后反代入W中,得展开后W能够表达成。其中a,b,c是固定值。这样,通过对W进行求导能够得到,然而要确保满足,我们使用表达求导求出来的,然而最后的,要根据下面状况得到:这样得到后,我们能够得到的新值。下面进入Platt的文章,来找到启发式搜索的办法和求b值的公式。这边文章使用的符号表达有点不太同样,但是实质是同样的,先来熟悉一下文章中符号的表达。文章中定义特性到成果的输出函数为与我们之前的实质是一致的。原始的优化问题为:求导得到:通过对偶后为:s.t.这里与W函数是同样的,只是符号求反后,变成求最小值了。和是同样的,都表达第i个样本的输出成果(1或-1)。通过加入松弛变量后,模型修改为:由公式(7)代入(1)中可知,这个过程和之前对偶过程同样。重新整顿我们规定的问题为:与之对应的KKT条件为:这个KKT条件阐明,在两条间隔线外面的点,对应前面的系数为0,在两条间隔线里面的对应为C,在两条间隔线上的对应的系数在0和C之间。将我们之前得到L和H重新拿过来:之前我们将问题进行到这里,然后说将用表达后裔入W中,这里将代入中,得其中这里的和代表某次迭代前的原始值,因此是常数,而和是变量,待求。公式(24)中的最后一项是常数。由于和满足下列公式由于的值是固定值,在迭代前后不会变。那么用s表达,上式两边乘以时,变为:其中代入(24)中,得这时候只有是变量了,求导如果的二阶导数不不大于0(凹函数),那么一阶导数为0时,就是极小值了。假设其二阶导数为0(普通成立),那么上式化简为:将w和v代入后,继续化简推导,得(推导了六七行推出来了)我们使用来表达:普通状况下目的函数是正定的,也就是说,能够在直线约束方向上求得最小值,并且。那么我们在(30)两边都除以能够得到这里我们使用表达优化后的值,是迭代前的值,。与之前提到的同样不是最后迭代后的值,需要进行约束:那么在特殊状况下,可能不为正,如果核函数K不满足Mercer定理,那么目的函数可能变得非正定,可能出现负值。即使K是有效的核函数,如果训练样本中出现相似的特性x,那么仍有可能为0。SMO算法在不为正值的状况下仍有效。为确保有效性,我们能够推导出就是的二阶导数,,没有极小值,最小值在边沿处取到(类比),时更是单调函数了,最小值也在边沿处获得,而的边沿就是L和H。这样将和分别代入中即可求得的最小值,对应的还是也能够懂得了。具体计算公式以下:至此,迭代关系式出了b的推导式以外,都已经推出。b每一...