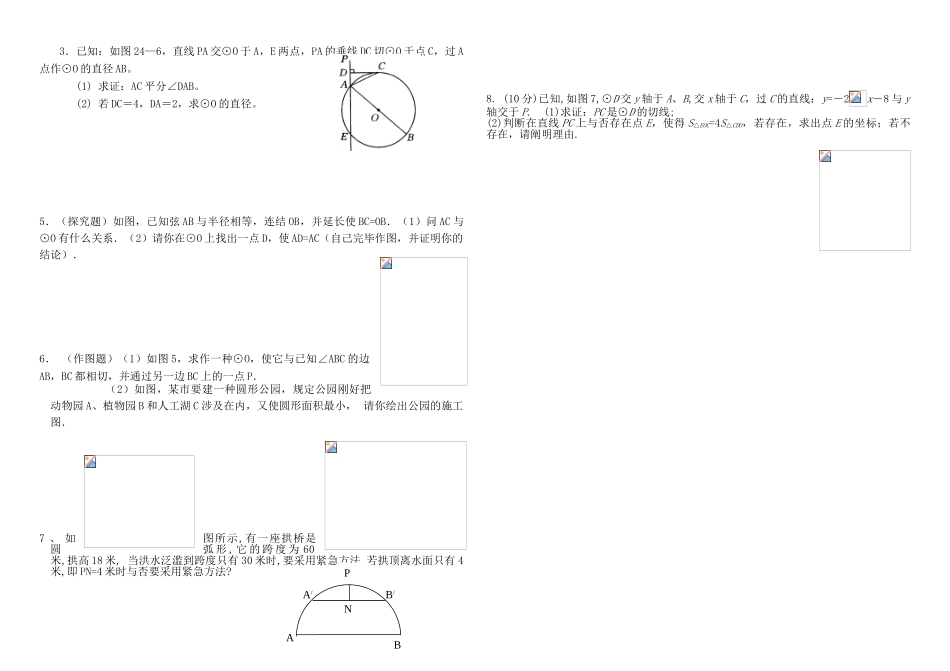
《圆》单元测试题一、选择题:1.下列五个命题:(1)两个端点能够重叠的弧是等弧;(2)圆的任意一条弧必然把圆分成劣弧和优弧两部分(3)通过平面上任意三点可作一种圆;(4)任意一种圆有且只有一种内接三角形(5)三角形的外心到各顶点距离相等.其中真命题有().A.1个B.2个C.3个D.4个2.如图1,⊙O外接于△ABC,AD为⊙O的直径,∠ABC=30°,则∠CAD=().A.30°B.40°C.50°D.60°(1)(2)(3)3.O是△ABC的外心,且∠ABC+∠ACB=100°,则∠BOC=().A.100°B.120°C.130°D.160°4.如图2,△ABC的三边分别切⊙O于D,E,F,若∠A=50°,则∠DEF=().A.65°B.50°C.130°D.80°5.Rt△ABC中,∠C=90°,AB=5,内切圆半径为1,则三角形的周长为().A.15B.12C.13D.146.在⊙O中,同弦所对的圆周角().A.相等B.互补C.互余D.相等或互补7.⊙O的半径为3cm,点M是⊙O外一点,OM=4cm,则以M为圆心且与⊙O相切的圆的半径一定是().A.1cm或7cmB.1cmC.7cmD.不拟定8.如图24—3所示,在△ABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若⊙O的圆心在线段BP上,且⊙O与AB,AC都相切,则⊙O的半径是().A.1B.C.D9.下列四个命题对的的是:①与圆有公共点的直线是切线;②垂直于圆的半径的直线是切线;③到圆心的距离等于半径的直线是切线;④过圆直径的端点,垂直于此直径的直线是切线A.①②B.②③C.③④D.①④10.⊙O的半径为6,⊙O的一条弦AB长为3,以3为半径的同心圆与直线AB的位置关系是()A.相离B.相切C.相交D.不能拟定11.I为△ABC的内心,如果∠ABC+∠ACB=100°,那么∠BIC等于()A.80°B.100°C.130°D.160°二、填空题.1.⊙O中,弦MN把⊙O分成两条弧,它们的度数比为4:5,如果T为MN中点,则∠TMO=______,则弦MN所对的圆周角为_______.2.⊙O到直线L的距离为d,⊙O的半径为R,当d,R是方程x2-4x+m=0的根,且L与⊙O相切时,m的值为_________.3.如图3,△ABC三边与⊙O分别切于D,E,F,已知AB=7cm,AC=5cm,AD=2cm,则BC=________.4.已知AB=10cm,点C在以AB为直径的⊙O上,AC=6cm,∠ACB的平分线交⊙O于D,则四边形ADBC的面积为5、在半径为1的圆中,长度等于的弦所对的圆心角是度。则⊙O的直径等于.6、若三角形面积为18,周长为36,则内切圆的半径为三、解答题.1.如图,从点P向⊙O引两条切线PA,PB,切点为A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm,求AC的长.2.如图,点P是圆上的一种动点,弦AB=√3,PC是∠APB的平分线,∠BAC=30°(1)当∠PAC等于多少度时,四边形PACB有最大面积?最大面积是多少?(2)当∠PAC等于多少度时,四边形PACB是梯形?阐明你的理由.54127943.已知:如图24—6,直线PA交⊙O于A,E两点,PA的垂线DC切⊙O于点C,过A点作⊙O的直径AB。(1)求证:AC平分∠DAB。(2)若DC=4,DA=2,求⊙O的直径。5.(探究题)如图,已知弦AB与半径相等,连结OB,并延长使BC=OB.(1)问AC与⊙O有什么关系.(2)请你在⊙O上找出一点D,使AD=AC(自己完毕作图,并证明你的结论).6.(作图题)(1)如图5,求作一种⊙O,使它与已知∠ABC的边AB,BC都相切,并通过另一边BC上的一点P.(2)如图,某市要建一种圆形公园,规定公园刚好把动物园A、植物园B和人工湖C涉及在内,又使圆形面积最小,请你绘出公园的施工图.7、如图所示,有一座拱桥是圆弧形,它的跨度为60米,拱高18米,当洪水泛滥到跨度只有30米时,要采用紧急方法,若拱顶离水面只有4米,即PN=4米时与否要采用紧急方法?8.(10分)已知,如图7,⊙D交y轴于A、B,交x轴于C,过C的直线:y=-2x-8与y轴交于P.(1)求证:PC是⊙D的切线;(2)判断在直线PC上与否存在点E,使得S△EOC=4S△CDO,若存在,求出点E的坐标;若不存在,请阐明理由.ABA/B/PN