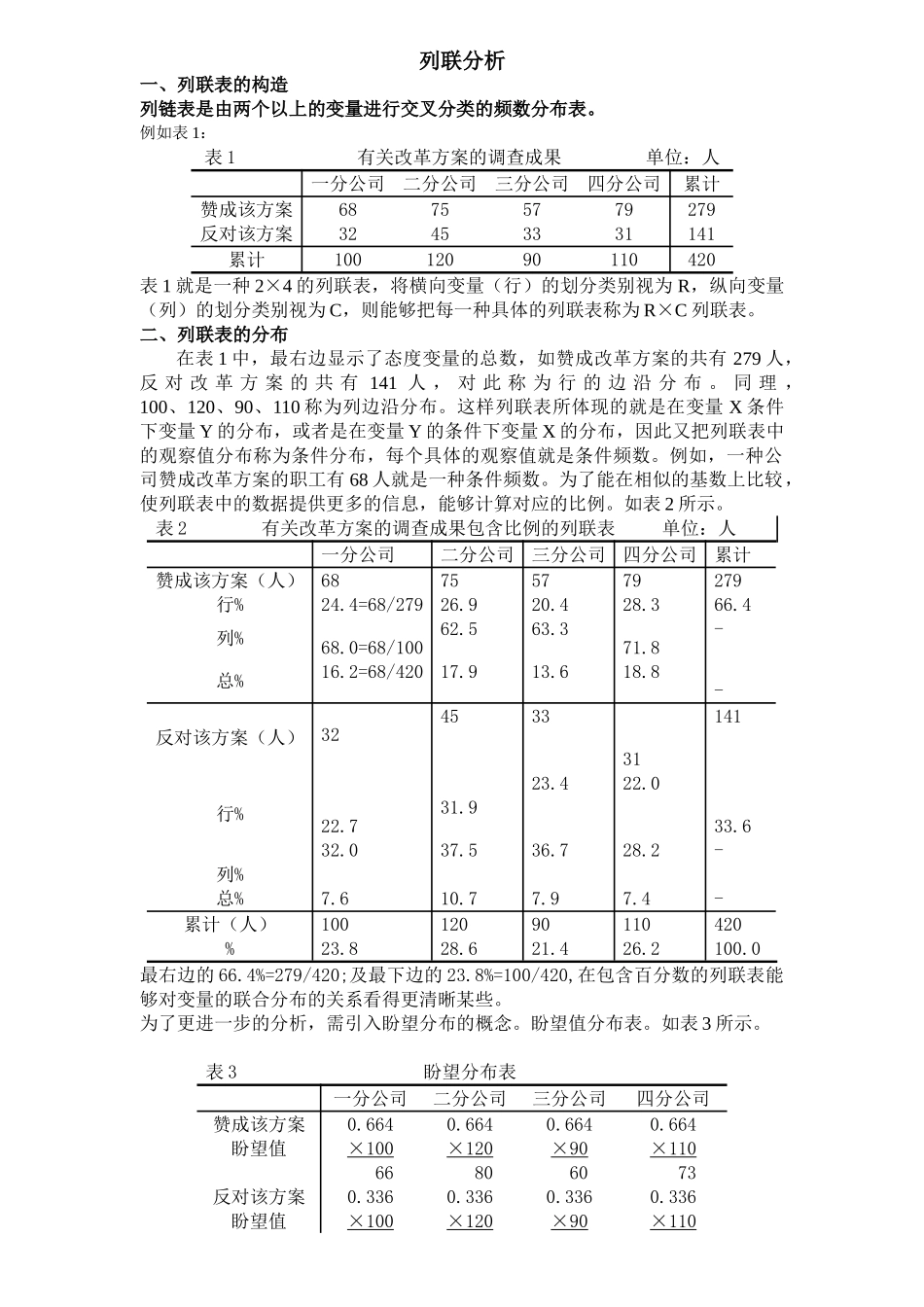
列联分析一、列联表的构造列链表是由两个以上的变量进行交叉分类的频数分布表。例如表1:表1有关改革方案的调查成果单位:人一分公司二分公司三分公司四分公司累计赞成该方案68755779279反对该方案32453331141累计10012090110420表1就是一种2×4的列联表,将横向变量(行)的划分类别视为R,纵向变量(列)的划分类别视为C,则能够把每一种具体的列联表称为R×C列联表。二、列联表的分布在表1中,最右边显示了态度变量的总数,如赞成改革方案的共有279人,反对改革方案的共有141人,对此称为行的边沿分布。同理,100、120、90、110称为列边沿分布。这样列联表所体现的就是在变量X条件下变量Y的分布,或者是在变量Y的条件下变量X的分布,因此又把列联表中的观察值分布称为条件分布,每个具体的观察值就是条件频数。例如,一种公司赞成改革方案的职工有68人就是一种条件频数。为了能在相似的基数上比较,使列联表中的数据提供更多的信息,能够计算对应的比例。如表2所示。表2有关改革方案的调查成果包含比例的列联表单位:人一分公司二分公司三分公司四分公司累计赞成该方案(人)68755779279行%24.4=68/27926.920.428.366.4列%68.0=68/10062.563.371.8-总%16.2=68/42017.913.618.8-反对该方案(人)32453331141行%22.731.923.422.033.6列%32.037.536.728.2-总%7.610.77.97.4-累计(人)10012090110420%23.828.621.426.2100.0最右边的66.4%=279/420;及最下边的23.8%=100/420,在包含百分数的列联表能够对变量的联合分布的关系看得更清晰某些。为了更进一步的分析,需引入盼望分布的概念。盼望值分布表。如表3所示。表3盼望分布表一分公司二分公司三分公司四分公司赞成该方案0.6640.6640.6640.664盼望值×100×120×90×11066806073反对该方案0.3360.3360.3360.336盼望值×100×120×90×11034403037在全部420个样本中,赞成改革方案的有279人,占总数的66.4%,那么对第一分公司来说,赞成该方案的人数应当为0.664×100=66人,66人即为盼望值。将观察值和盼望值频数结合在一起,就能够得到观察值和盼望值对比分布表,如表4所示。表4观察值和盼望频数对比分布表一分公司二分公司三分公司四分公司赞成该方案观察值68755779盼望值66806073反对该方案观察值32453331盼望值34403037如果各个分公司对改革方案的见解相似,即各分公司赞成改革方案的比例相似就应当有(为第个分公司赞成改革方案的比例),对于需要验证这一假设,能够采用分布进行检查。三、统计量能够用于变量间拟合优度检查和独立性检查,能够运用测定两个分类变量之间的有关程度。若用表达观察值频数,用表达盼望值频数,则统计量为:计算统计量的环节(可见表5):环节一:用观察值减去盼望值。环节二:将之差平方。环节三:将平方成果除以。环节四:将环节三的成果加总。表5计算表/6866240.0606067580-5250.31255760-390.1579736360.4931513234-240.11764745405250.6253330390.33137-6360.9729733.031877=3.0319统计量有这样几个特性:首相0,由于它是对平方值成果的汇总。另首先,值的大小与观察值和盼望值的配对数,即R×C的多少有关。R×C越多,在不变化分布的状况下,值越大,因此,统计量的分布与自由度有关。最后,统计量描述了观察值与盼望值的靠近程度。如果两者越靠近,即的绝对值越小,计算出的值越小。自由度的计算公式:(随着自由度的增大,分布将趋近对称的正态分布)自由度=(行数-1)(列数-1)=(R-1)(C-1)四、拟合优度检查若要对多个比例与否相等进行检查,就需要运用检查的办法,如果样本是从总体的不同类别中分别抽取,研究目的是对不同类别的目的量之间与否存在明显性差别进行检查,称为拟合优度检查,或一致性检查。在前面的例子中,计算的=3.0319,在0.1的明显性水平下检查四个分公司对改革方案与否存在差别。的自由度为(2-1)(4-1)=3,因此查的临界值=6.251。由于,故不能回绝原假设,即认为四个公司对改革方案的赞成比例是一致的()调查数据中的差别是由抽样的随机性造成的。拟合优度检查的另外一种状况是运用样本数据检查总体比例与否等于某个数例:为了提高市场占有率,某行业两个最重要的竞争对手A公...