高一数学 (函数y=Asin(ωxφ)的图象) 课件VIP免费

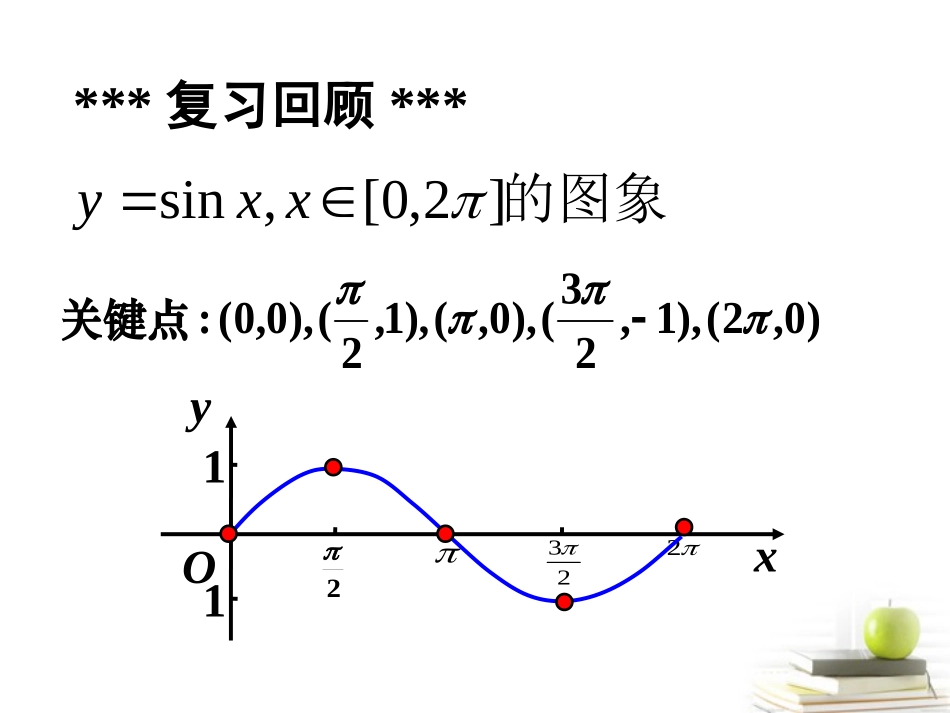
2yxO11232)0,2(),1,23(),0,(),1,2(),0,0(:关键点***复习回顾***的图象]2,0[,sinxxy)(A置的最大距离运动的物体离开平衡位：振幅)(2TT次所需要的时间运动的物体往复运动一＝：周期)(21内往复运动的次数运动的物体在单位时间＝：频率Tff称为初相时的相位：相位0xx:)0,0)(sin(运动中的相关概念在简谐其中AxAy物理中简谐振动的相关物理量试研究与的图象关系.xysin)6sin(),3sin(xyxy23632y1-1Ox223352613xysin)3sin(xy)6sin(xy探究1：对函数图象的影响21-1xysinoxy22332635613)6sin(xyxysinxysinxysinxysinxysinxysinxysinxysin)3sin(xyxysinxysinxysinxysinxysin32一、函数y=sin(x+)图象:的变化引起图象位置发生变化(左加右减)平移变换①把y=sinx的图象向__(φ>0时)或向___(φ<0时)平移|φ|个单位长度得到y=sin(x+φ)的图象.左右函数y=3cos(x+)图象向左平移个单位所得图象的函数表达式为_____43把y=sin2x的图象经过怎样的变换就得到y=sin(2x+)的图象?3想一想?作函数及的图象.xy21sinxy2sinx2x2sin2234243x21sinxx223x21yOx-1-12211323222525233727244443434xy21sinxy2sinxysin探究探究22：：对函数图象的影响对函数图象的影响函数、与的图象间的变化关系.xy21sinxysinxy2sin-12yOx241xy21sinxy2sin二、函数y=sinx(>0)图象:周期变换2T决定函数的周期:②把所得图象各点的横坐标____(ω>1时)或___(0<ω<1时)到原来的___倍(纵坐标不变),得到y=sin(ωx+φ)的图象.缩短伸长1/ω为了得到y=3sin(2x+π/5)的图象,只需将函数y=3sin(x+π/5)的图象上各点的()而得到.A.横坐标伸长到原来的2倍,纵坐标不变.B.横坐标缩短到原来的1/2倍,纵坐标不变.D.纵坐标伸长到原来的2倍,横坐标不变.C.纵坐标伸长到原来的1/2倍,横坐标不变.By=Asinx与y=sinx的图象关系:xysin21xysin22sinxsinxxxsin210223200011000220002121作下列函数图象:xO1-1y2-222323222xysin2xysin21xysin探究3：A对函数图象的影响函数、与的图象间的变化关系.xysin21xysinxysin2xO1-1y2-22232xysin2xysin21振幅变换y=sinxy=Asinx所有的点纵坐标伸长(A>1)或缩短(00)图象:A的大小决定这个函数的最大(小)值上述变换称为振幅变换，据此理论，函数的图象是由函数的图象经过怎样的变换而得到的？)43sin(23xy)43sin(xy用“五点法”画出函数y=3sin(2x+π/3)的简图.解:651273126x2232032x-3ox222312-1-23y63π12653sin(2x+π/3)030-30)3/2sin(x-11000思考:如何由变换得的图象？xysin)32sin(3xy1-12-2ox3-36536335612767322y方法1:(按先平移后变周期的顺序变换))32sin(3xy)32sin(xyxysin)3sin(xyy=sinxy=sin(x+)横坐标缩短>1(伸长0<<1)到原来的1/倍y=sin(x+)纵坐标伸长A>1(缩短00(向右<0)方法1:按先平移后变周期的顺序变换平移||个单位纵坐标不变横坐标不变1-12-2ox3-36536335612767322y方法2:(按先变周期后平移顺序变换)xy2sin)32sin(xy)32sin(3xyxysin)6(2sin)32sin(xxyy=sinx横坐标缩短>1(伸长0<<1)到原来的1/倍y=sinx纵坐标伸长A>1(缩短00(向右<0)平移||/个单位)sin()(sinxxy如何由y=sinx的图象得到y=3sin(x-)的图象?214向右平移π/4...