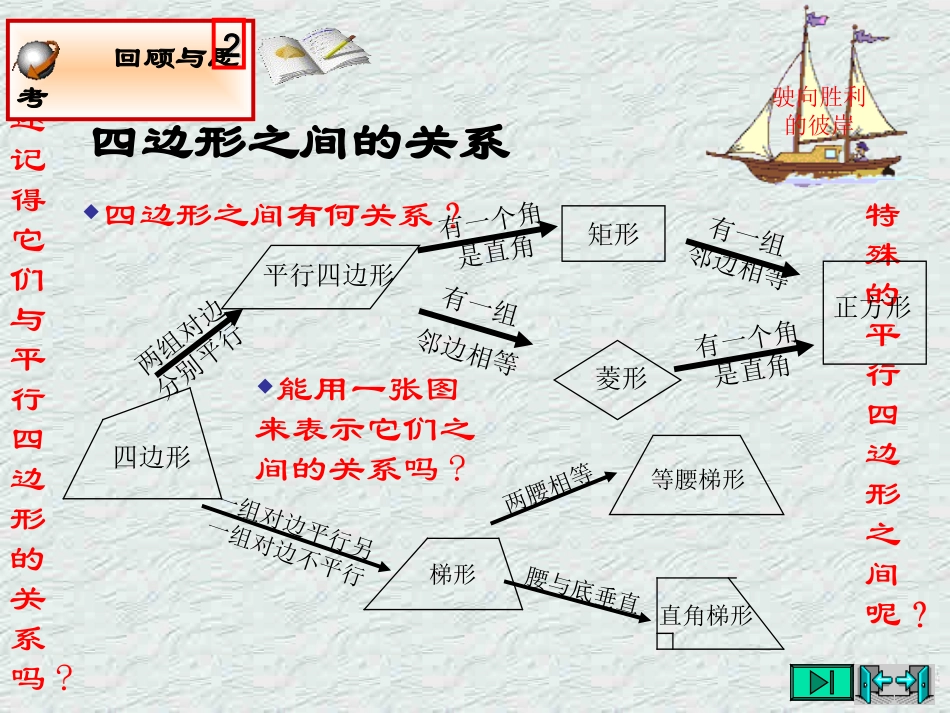
九年级数学(上)第三章证明(三)特殊的平行四边形驶向胜利的彼岸学好几何标志是会“证明”证明命题的一般步骤:(1)理解题意:分清命题的条件(已知),结论(求证);(2)根据题意,画出图形;(3)结合图形,用符号语言写出“已知”和“求证”;(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”);(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;(6)检查表达过程是否正确,完善.回顾与思考11驶向胜利的彼岸四边形之间的关系四边形之间有何关系?特殊的平行四边形之间呢?还记得它们与平行四边形的关系吗?能用一张图来表示它们之间的关系吗?四边形平行四边形矩形菱形正方形两组对边分别平行有一个角是直角有一组邻边相等有一个角是直角有一组邻边相等一组对边平行另一组对边不平行梯形两腰相等等腰梯形腰与底垂直直角梯形回顾与思考22驶向胜利的彼岸平行四边形的性质与判定回顾与思考33性质判定边角对角线推论平行四边形的①两组对边分别平行②两组对边分别相等平行四边形的①对角相等②邻角互补平行四边形的对角线互相平分夹在两条平行线间的平行线段相等①两组对边分别平行的四边形②两组对边分别相等的四边形③一组对边平行且相等的四边形两组对角分别相等的四边形对角线互相平分四边形BDCAOBDCAMNPQ驶向胜利的彼岸等腰梯形的性质与判定回顾与思考44性质判定边角对角线两底平行,两腰相等等腰梯形同一底上的两个角相等等腰梯形的两条对角线相等两腰相等的梯形是等腰梯形同一底上的两个角相等的梯形是等腰梯形两条对角线相等的梯形是等腰梯形BDCABDCA三角形中位线的性质驶向胜利的彼岸定理:三角形的中位线平行于第三边,且等于第三边的一半.这个定理提供了证明线段平行,和线段成倍分关系的根据. DE是△ABC的中位,DEBCA.21BCDE∴DE∥BC,回顾与思考55三角形中位线的性质驶向胜利的彼岸模型:连接任意四边形各边中点所成的四边形是平行四边形.这个定理提供了证明线段平行,和线段成倍分关系的根据.要重视这个模型的证明过程反映出来的规律:对角线的关系是关键.改变四边形的形状后,对角线具有的关系(对角线相等,对角线垂直,对角线相等且垂直)决定了各中点所成四边形的形状.ABCHDEFG回顾与思考66矩形的性质定理:矩形的四个角都是直角.驶向胜利的彼岸试一试P8611已知:如图,四边形ABCD是矩形.分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.证明: 四边形ABCD是矩形,∴∠A=900,四边形ABCD是平行四边形.∴∠C=∠A=900,∠B=1800-∠A=900,∠D=1800-∠A=900.求证:∠A=∠B=∠C=∠D=900.∴四边形ABCD是矩形.DBCA想一想:正方形的四个角都是直角吗?矩形的性质驶向胜利的彼岸定理:矩形的两条对角线相等.已知:如图,AC,BD是矩形ABCD的两条对角线.求证:AC=BD.证明: 四边形ABCD是矩形,∴AB=DC,∠ABC=∠DCB=900.分析:根据矩形的性质性质,可转化为全等三角形(SAS)来证明.DBCA BC=CB,∴△ABC≌△DCB(SAS).∴AC=DB.试一试P8622直角三角形的性质驶向胜利的彼岸议一议:设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段?它与AC有什么大小关系?为什么?DBCAE由此可得推论:直角三角形斜边上的中线等于斜边的一半.BE是Rt△ABC中斜边AC上的中线.BE等于AC的一半. AC=BD,BE=DE,.21BDBE.21ACBE议一议P8633矩形性质的应用驶向胜利的彼岸例题欣赏P8644已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相交于点O,∠AOD=1200,AB=2.5cm.求矩形对角线的长.解: 四边形ABCD是矩形,∴BD=2AB=2×2.5=5(cm)..21ACOCOA∴AC=BD,且 ∠DAB=900,DBCAO.21BDODOB.ODOA ∠AOD=1200,.302120180000∴∠ODA=∠OAD=你认为例1还可以怎么去解?矩形---?---正方形1.正方形的四个角都是直角吗?驶向胜利的彼岸已知:如图,在四边形ABCD中,∠A=∠B=∠C=900.分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.证明: ∠A=∠B=∠C=900,∴∠A+∠B=18000,∠B+∠C=1800.∴AD∥BC,AB∥CD.求证:四边形ABCD是矩形.∴四边形ABCD是平行四边形.∴四边形ABCD是矩形.随堂练习P8844DBCA矩形的判定2.定理:有三个角是直角的...