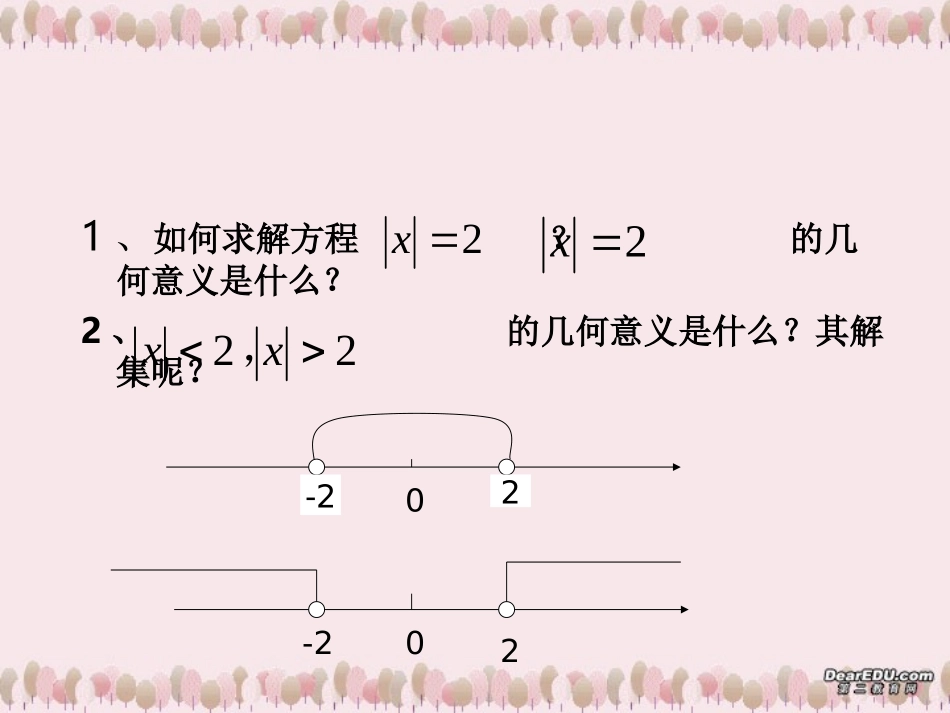
1.4含绝对值的不等式解法)0(,ccbaxcbax复习回顾1、不等式的基本性质:若a>b,则a+c>b+c;若a>b,c>0,则ac>bc;若a>b,c<0,则ac
1或2x-3<-1解得x>2或x<1所以,原不等式的解集为{x|x>2或x<1}。归纳:形如型不等式的解法。1、将ax+b看成整体,化归转化成|x|<a或|x|>a的形式。一般地,|ax+b|>c(c>0)的解法是:先化原不等式为不等式组ax+b>c或ax+b<-c,再由不等式的性质求出原不等式的解集。|ax+b|0)的解法是:先化原不等式为不等式组-c0,n>0)型不等式的解法。例2、解不等式1<|2x+1|<3。解:原不等式可化为解不等式1,得-3<2x+1<3,所以,得-21,或2x+1<-1所以,得x>0,或x<-1所以原不等式的解集为{x|-2<x<1}{x|x>0或x<-1}即{x|0<x<1,或-2<x<-1}112312xx12对于双边不等式m<|ax+b|0,n>0)一种方法是根据绝对值的定义分两种情况去掉绝对值符号;第二种方法可先将不等式转化为与之等价的不等式组,进而再利用|ax+b|>c(c>0),或|ax+b|0)型不等式的解法逐一求解。3、形如|ax+b|mx+n(其中m、n为常数,且m不为0)型不等式的解法。例3、解不等式|2x+1|>x+1解:原不等式可化为2x+1>x+1,或2x+1<-(x+1)解得x>0,或x<-2/3所以,原不等式的解集为{x|x>0或x<-2/3}例4、解不等式|x-1|+|2-x|>3+x解:把原不等式变形为|x-1|+|x-2|>3+x若|x-1|=0,x=1;若|x-2|=0,x=2。这样1,2把数轴分成了三个部分,如图(1)当x1时,x-10,x-2<0,所以,原不等式变形为-(x-1)-(2-x)>3+x,即x<0。此时,得{x|x1}{x|x<0}={x|x<0}(2)当10,x-20,所以,原不等式变形为x-1-(x-2)>3-x,即x<-2。此时,得{x|12时,x-1>0,x-2>0,所以,原不等式变形为x-1+x-2>3+x,即x>6。此时,得{x|x>2}{x|x>6}={x|x>6}将(1)(2)(3)取并集,得原不等式的解集为{x|x<0,或x>6}012含有多个绝对值(二个或二个以上)的不等式的解法(1)找零点(2)划区间(3)分段讨论(4)求各段结果的并集零点分段讨论法1、含有绝对值的不等式解法的关键是去掉绝对值符号;2、注意在解决问题过程中绝对值不等式的几何意义。作业:1、优化P157、8、9、102、补充题:(1)解不等式|ax+3|<2(a不为0)(2)解不等式|x+3|+|x+2|+|x+1|>3