椭圆 高二数学椭圆课件 新课标 高二数学椭圆课件 新课标VIP免费

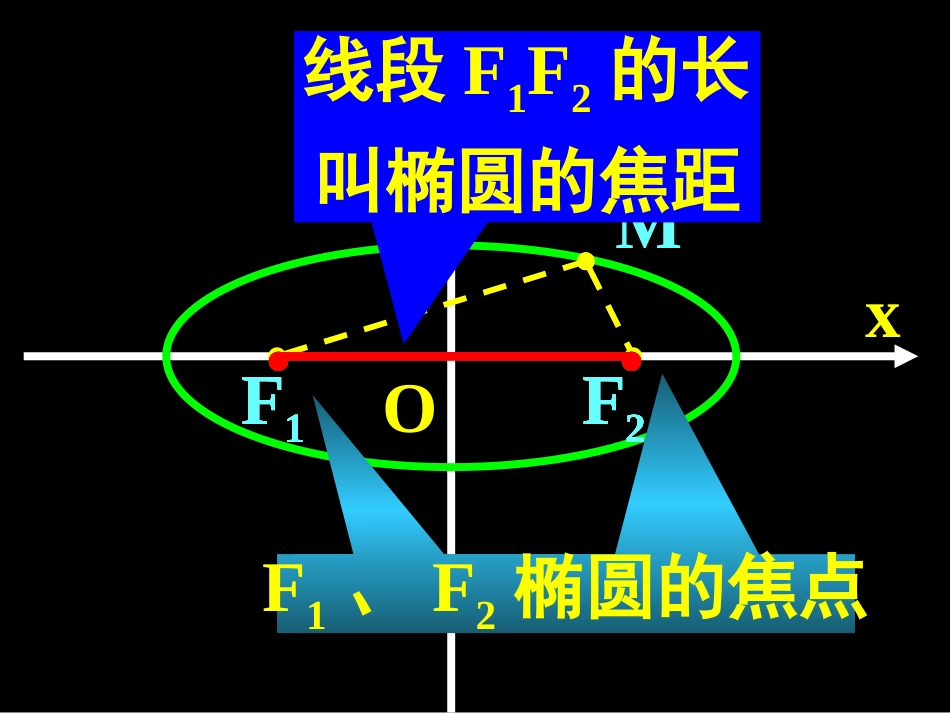
平面内与两个定点F1、F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆.OxyMF1F2••F1F2••F1、F2椭圆的焦点F1F2••F1F2••F1F2••F1F2••F1F2••线段F1F2的长叫椭圆的焦距椭圆的标准方程椭圆的标准方程::((焦点在焦点在xx轴上轴上)).babyax012222OxyF2F1M椭圆的标准方程椭圆的标准方程::((焦点在焦点在yy轴上轴上)).babxay012222椭圆的几何性质：1.范围:byaxbyaxbyaxyx,.,,1,1,),(22222222即必有是椭圆上任意一点设.所围成的矩形内，椭圆在四条直线byaxB2B1A1A2F1F2xyOabc)0(12222babyax椭圆的几何性质：2.对称性:..成中心对称关于原点轴成轴对称轴、关于Oyx椭圆的几何性质：3顶点:坐标轴与椭圆的四个交点叫做顶点.,0;,0;0,;0,2121bBbBaAaA椭圆的几何性质：4.离心率:.,,0,0.,0,,1.100.2222椭圆越圆从而时当椭圆越扁从而时当叫做椭圆的离心率，比椭圆的焦距与长轴长的abcecabaceecaacace椭圆的准线定义:..,.),1(是椭圆的离心率常数的准线定直线是椭圆定点是椭圆的焦点此动点的轨迹是椭圆是常数一条定直线的距离的比和它到动点与一个定点的距离eeacecaxl2:M(x,y)FNdOyxFcaxl2/:椭圆的准线2200椭圆的几何性质椭圆的几何性质2001.32001.3例5如图，以原点为圆心，分别以a,b(a>b>0)为半径作两个圆，点B是大圆半径OA与小圆的交点，过点A作BM⊥OX,垂足为M,求当半径OA绕点O旋转时点M的轨迹的参数方程。1、求适合下列条件的椭圆的标准方程：（1）椭圆经过两点)5,0(Q);0,22(P15822yx（2）长轴是短轴的3倍，椭圆经过点P（3，0）；（3）离心率等于0.8，焦距是8；181922yx1922yx192519252222xyyx或).6,5(P),0,32()0,32()4(并且经过点和焦点坐标是182022yx2、求下列椭圆的离心率：（1）从焦点看短轴两端点的视角为60°；（2）从短轴的一个端点看两焦点的视角为直角。2322OyxF2F1OxF2F1yB3、点P与一定点F（2，0）的距离和它到一定直线x=8的距离的比是1：2，求点P的轨迹方程，并说明轨迹是什么图形。1121622yx6、已知椭圆F1，F2是它的焦点，AB是过F1的弦，则三角形ABF2的周长是（）)0ba(1byax22224aOxyF1F2AB7、如果椭圆的两个焦点将长轴三等分，那么这个椭圆的两条准线间的距离是焦距长的（）倍。98、椭圆上一点P到左准线的距离是5/2，那么P点到右焦点的距离是（）19y25x228lF1F2POxy:,5518,52.9是则椭圆方程距离是准线间椭圆焦距为14x9y;14y9x222210、椭圆中心在原点，它在x轴上的一个焦点与短轴两端点的连线互相垂直，且此焦点和长轴上较近端点的距离是求椭圆方程。510151022yx11、在椭圆上求一点，使它与两焦点连线互相垂直。120y45x22A(3,4）B(-3,4)C(-3,-4)D(3,-4)4、三角形ABC的一边的两顶点是B（0，6）和C（0，-6），另两边的斜率乘积是-4/9，求顶点A的轨迹。12、直线xcos+ysin=2（0）与椭圆有公共点，求的取值范围。6y3x2213、我国发射的第一颗人造地球卫星的运行轨道，是以地球的中心F2为一个焦点的椭圆，近地点A距地面439公里，远地点B距地面2384公里，地球半径约为6371公里。求卫星轨道方程。OF1F2AxyB解：a-c=|OA|-|OF2|=|F2A|=6371+439=6810，a+c=|OB|+|OF2|=|F2B|=6371+2384=8755解得：a=7782.5，c=972.517722y7783x:5.772168108755)ca)(ca(cab222222因此卫星轨道方程是例例2求适合下列条件的椭圆的标准方程（1）经过点P（3，0）、Q（0，-2）；（2）长轴的长等于20，离心率等于3/5。例25、点M与椭圆的左焦点和右焦点的距离的比为2：3，求点M的轨迹方程。112y13x2222