高中数学 椭圆的定义与标准方程课件 新人教版选修1 1 课件VIP免费

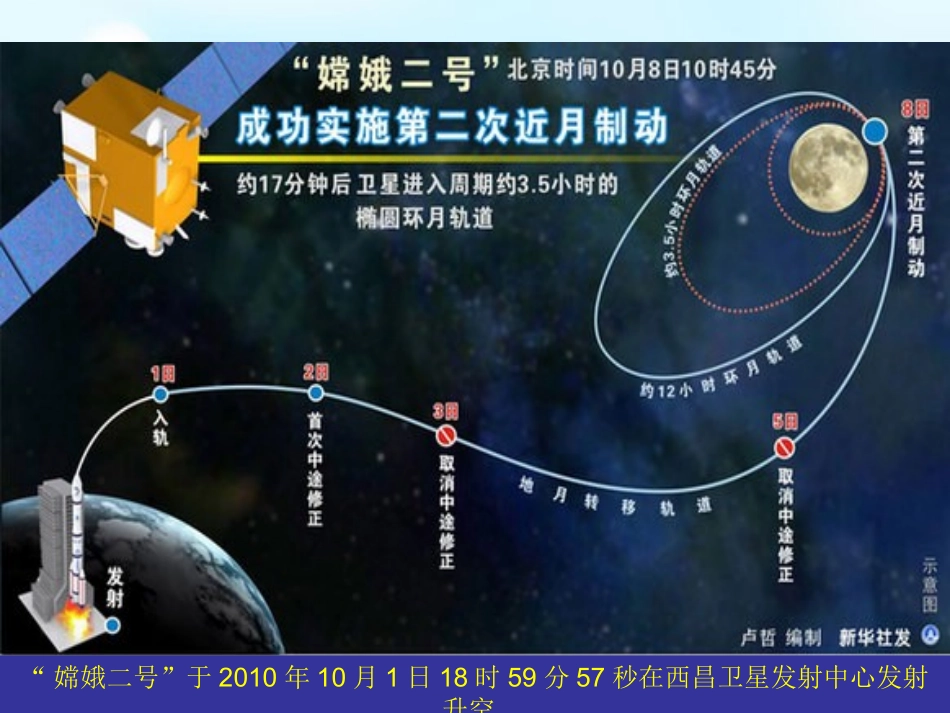
2.2.1椭圆及其标准方程第一课时“嫦娥二号”于2010年10月1日18时59分57秒在西昌卫星发射中心发射升空太阳系♦自然界处处存在着椭圆,我们如何用自己的双手画出椭圆呢?实验探究：（1）取一条定长的细绳,把它的两端都固定在画板的同一点上，套上铅笔，拿紧绳子，移动笔尖。（2）若把细绳的两端拉开一段距离，分别固定在图板的两点处，套上铅笔，拿紧绳子，移动笔尖，实验演示椭圆的定义椭圆的定义•平面上到两个定点的距平面上到两个定点的距离的和（离的和（22aa）等于定）等于定长（长（大于大于|F|F11FF22||）的）的点的轨迹叫点的轨迹叫椭圆椭圆。。•定点定点FF11、、FF22叫做叫做椭圆椭圆的焦点的焦点。。•两焦点之间的距离叫做两焦点之间的距离叫做焦距焦距（（2c2c）。）。椭圆定义的文字表述：椭圆定义的符号表述：122(22)MFMFaac1.改变两定点之间的距离，使其与绳长相等，画出的图形还是椭圆吗？2．绳长能小于两图钉之间的距离吗？1.改变两定点之间的距离，使其与绳长相等，画出的图形还是椭圆吗？2．绳长能小于两图钉之间的距离吗？OxyF1F2M如图所示:F1、F2为两定点，且|F1F2|=2c，求平面内到两定点F1、F2距离之和为定值2a(2a>2c)的动点M的轨迹方程。解：以F1F2所在直线为x轴，线段F1F2的垂直平分线为y轴建立直角坐标系，(-c,0)(c,0)(x,y)设M（x,y)为所求轨迹上的任意一点，则椭圆就是集合P={M||MF1|+|MF2|=2a}aycxycx2)()(2222即2222)(2)(ycxaycx如何化简?则焦点F1、F2的坐标分别为(-c,0)、(c,0)。问题:求曲线方程的基本步骤？（1）建系;（2）设点；（3）写出限制条件；（4）代入点的坐标；（5）化简方程。OxyF1F2M(-c,0)(c,0)(x,y)整理，得(a2-c2)x2+a2y2=a2(a2-c2) 2a>2c>0，即a>c>0，∴a2-c2>0，(a>b>0)2222)(2)(ycxaycx2222222)()(44)(ycxycxaaycx则222)(ycxacxa整理得2222222222422yacacxaxaxccxaa两边平方得：两边同除以a2(a2-c2)得:122222cayaxP,||||,||||2121cOFOFaPFPF可得22||caPO22||caPOb令那么①式12222byax如图点P是椭圆与y轴正半轴的交点①你能在图中找出表示a，c，，的线段吗？22ac,,abc怎样判断大小关系？OxyF1F2MOxyF1F2M22221(0)xyabab22221(0)yxabab222cab这里222cab这里)0,(),0,(21cFcF焦点),0(),,0(21cFcF焦点2.椭圆的标准方程思考：方程Ax2+By2=C何时表示椭圆？答：A、B、C同号且A、B不相等时。思考二:如何由标准方程判定焦点位置?x2与y2的分母哪一个大，则焦点在哪一个轴上.2222+=1>>0xyabab2222+=1>>0xyabba分母哪个大，焦点就在哪个轴上222=+abc平面内到两个定点F1，F2的距离的和等于常数（大于F1F2）的点的轨迹12-,0,0，FcFc120,-0,，FcFc标准方程不同点相同点图形焦点坐标定义a、b、c的关系焦点位置的判断♦再认识！xyF1F2POxyF1F2PO预习自测1、指出下列方程中的,,abc的值，焦点的位置和坐标。⑴22194yx；⑵22194yx；⑶221916yx；⑷228324xy3,2,5(50)(5(0).1)abcx-轴上，，，，3,2,5(05).(2)abcy轴上，，4,3,7(07)(0(7).3)abcy-轴上，，，，2,3,(0).(4)abcy255轴上，，2、椭圆192522yx上一点P到一个焦点的距离为4，则P到另一个焦点的距离为（）A、5B、6C、4D、103、写出适合下列条件的椭圆的标准方程：（1）a=4,b=3,焦点在x轴；（2）a=6,c=1焦点在y轴上（3）两个焦点坐标分别是(-4,0)、（4，0），椭圆上一点P到两焦点的距离之和等于10；B221169xy2213536xy221259xy例.已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点,求它的标准方程.5(,23)2解法一:因为椭圆的焦点在x轴上,所以设它的标准方程为).0(12222babyax(3,0),(3,0)又焦点的坐标分别是3c229ab225222()(23)1ab又由已知①②联立①②,222516ab解得，因此,所求椭圆的标准方程为221.2516xy求椭圆标准方程的解题步骤：（1）确定焦点的位置；（2）设出椭圆的标准方程；（3）用待定系数法确定a、b...