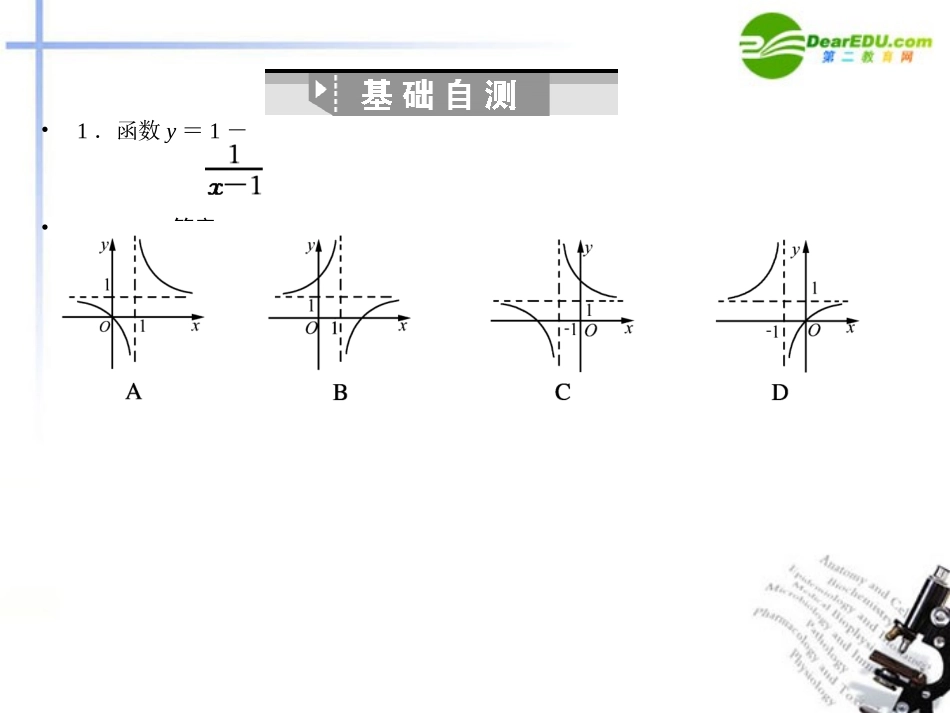
•掌握作函数图象的基本方法/能利用函数图象分析解决问题第10课时函数图象•1.作图方法:描点法和利用基本函数图象变换作图;作函数图象的步骤:①确定函数的定义域;②化简函数的解析式;③讨论函数的性质即单调性、奇偶性、周期性、最值(甚至变化趋势);④描点连线,画出函数的图象.•2.三种图象变换:平移变换、对称变换和伸缩变换.•3.识图:对于函数的图象要注意其分布范围、变化趋势、对称性、周期性等方面.•4.用图:函数的图象形象地显示了函数的性质,为研究数量关系提供了“形”的直•观性,它是探求解题途径,获得问题结果的重要工具,要重视数形结合思想方法•的运用.•1.函数y=1-的图象是()•答案:B•2.函数y=e|lnx|-|x-1|的图象大致是()••答案:D•3.(2009·重庆模拟)已知图①中的图象对应的函数为y=f(x),则图②的图象对应的函数为()••A.y=f(|x|)B.y=|f(x)|C.y=f(-|x|)D.y=-f(|x|)•答案:C•4.(2009·湖南)如图,当参数λ=λ1,λ2时,连续函数•y=(x≥0)的图象分别对应曲线C1和C2,则()•A.0<λ1<λ2B.0<λ2<λ1•C.λ1<λ2<0D.λ2<λ1<0•解析:令x=x0(x0>0),由图象可知,•,λ1x0>λ2x0,(λ1-λ2)x0>0,•λ1>λ2,又因为函数y=在(0,+∞)连续,因此λ>0,故选B.•答案:B•作函数图象首先要明确函数图象的位置和形状,然后借助描点等手段作出•函数图象,而明确函数图象位置和形状的主要方法有:•(1)图象的变换,例如y=|x|=y==+1等.•(2)等价变形,如y=,等价于•(3)研究函数的性质.•【例1】作出下列函数的图象:•解答:(1)解法一:函数的定义域为(∞-,-1)(∪-1,1)(1∪∞,+),且函数为偶函数,函数的递增区间为(∞-,-1),(-1,0),递减区间为(0,1),(1,∞+).•可根据以上性质取值列表:•在直角坐标系中描出上表对应点并用光滑的曲线连结起来.再根据y=是偶函数,把所作图象关于y轴对称到y轴左侧后,就得到y=的图象(如图1).•当x≥0且x≠1时,y=,它的图象可由y=的图象向右平移一个单位后得到(仅要y轴及其右侧部分).•当x<0且x≠-1时,y=-,它的图象可由y=的图象先关于x轴对称后,再向左平移一个单位后得到(仅要y轴左侧部分),把上述两次得到的图象合在一起就得到函数y=的图象(如图1).图1•解法三:作函数图象还可通过求导确定函数的单调性和极值情况:当x≥0时,•y=,求导得y′=<0,∴单调递减区间是[0,1)及(1,+∞),取•x=在坐标系中描出各点并用光滑曲线连结起来,再把•所得曲线关于y轴对称就得到函数y=的图象(如图1).•(2)当x≥0时,f(x)=x2-2x-1=(x-1)2-2,当x<0时,•f(x)=x2+2x-1=(x+1)2-2,即f(x)=•根据二次函数的作图方法,可得函数图象如图2.•(3)若x≥2,原式为y==-x(x≠4),•若x<2,原式为y==x-4(x≠0),故所求图象如图3所示.图3图2•所以原函数是以(-1,2)为中心,以直线x=-1、y=2为渐近线的反比例函数,•其图象如图4所示.图4•对于给定函数的图象,可从图象上下左右分布范围,变化趋势,特殊点的坐标等方面进行判断,必要时可借助解方程、解(证)不等式等手段进行判断,未必非要写出函数的解析式进行判断.•【例2】回答下述关于图象的问题:•(1)向形状如右图,高为H的水瓶注水,注满为止,若将注水量V看作水深h的函数,则函数V=f(h)的图象是下图中的()•(2)某学生一天早晨离家去学校,开始骑自行车,中途自行车胎破,他只好推着自行车赶到学校.若将这天早晨他从家里出来后离学校的距离d表示为他出发后的时间t的函数d=f(t),则函数f(t)的大致的图象是下图中的()•解析:(1)水量V显然是h的增函数,将容器的高等分成n段,每一段记为Δh,从开始注水起(即从下到上)计算,每段Δh对应的水量分别记为ΔV1,ΔV2,…,ΔVn,由于容器上小下大,∴ΔV1>ΔV2>…>ΔVn,即当h愈大时,相等高度增加的水量愈少,∴其图象呈“上凸”形状,故选A.•(2) 时间t愈大,该学生离学校的距离d愈小,∴d是t的减函数,答案应为C、D中的一个,由于前一段时间速度快,后一段时间速度慢,即的值前大后小,故选D.•答案:(1)A...