高中数学第三章极大值与极小值1课件苏教版选修1-1 课件VIP免费

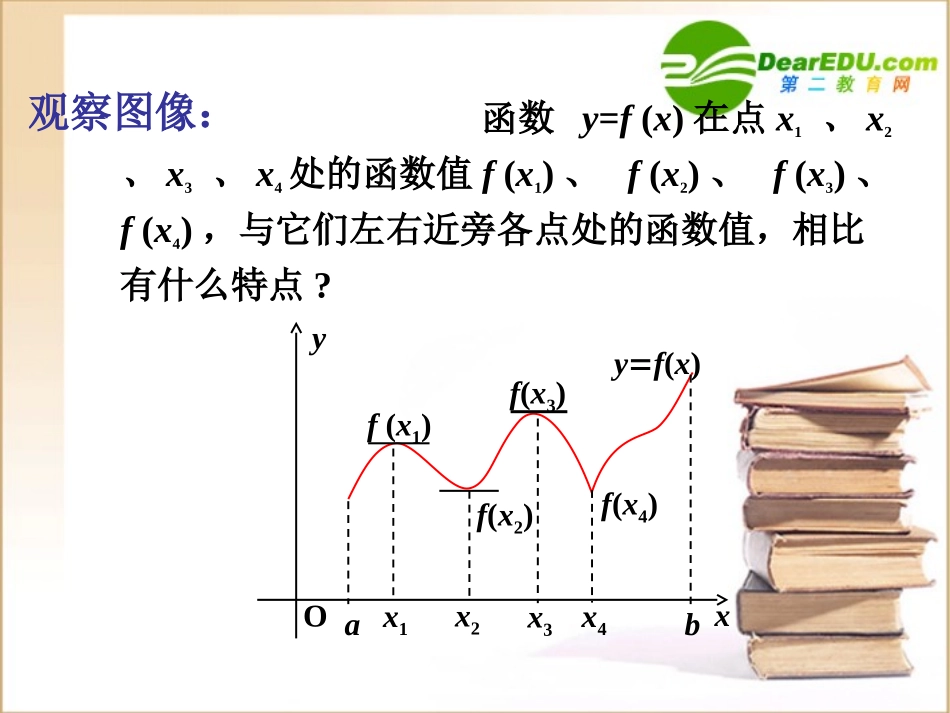
3.3.2极大值与极小值单调性与导数的关系：设函数y=f(x)在某个区间内可导，•如果f′(x)>0，则f(x)为增函数；•如果f′(x)<0，则f(x)为减函数；•如果f′(x)=0，则f(x)为常数函数；复习:yxOabyf(x)x1f(x1)x2f(x2)x3f(x3)x4f(x4)函数y=f(x)在点x1、x2、x3、x4处的函数值f(x1)、f(x2)、f(x3)、f(x4)，与它们左右近旁各点处的函数值，相比有什么特点?观察图像：一、函数的极值定义一般的，设函数f(x)在点x0附近有定义，•如果对X0附近的所有点，都有f(x)f(x0),则f(x0)是函数f(x)的一个极小值，记作y极小值=f(x0)；oxyoxy0x0x◆函数的极大值与极小值统称为极值.(极值即峰谷处的值------不一定最大或最小）使函数取得极值的点x0称为极值点数学建构（3）极大值与极小值没有必然关系，极大值可能比极小值还小.注意：oax1x2x3x4bxyP(x1,f(x1))y=f(x)Q(x2,f(x2))（1）极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;（2）函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值；yxO观察与思考：极值与导数有何关系？在极值点处，曲线如果有切线，则切线是水平的。abyf(x)x1f(x1)0x2f(x2)0x3f(x3)0x4f(x5)0x5观察图像并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系?oax0bxyxx0左侧x0x0右侧f(x)f(x)oax0bxyxx0左侧x0x0右侧f(x)f(x)增f(x)>0f(x)=0f(x)<0极大值减f(x)<0f(x)=0增减极小值f(x)>0数学建构请问如何判断f(x0)是极大值或是极小值？f(x)<0yxOx1abyf(x)在极大值点附近在极小值点附近f(x)<0f(x)>0f(x)>01、如果在x0附近的左侧f’(x)>0，右侧f’(x)<0，则f(x0)是极大值；2、如果在x0附近的左侧f’(x)<0，右侧f’(x)>0，则f(x0)是极小值；已知函数f(x)在点x0处是连续的，则二、判断函数极值的方法x2左正右负为极大，右正左负为极小注意：函数极值是在某一点附近的小区间内定义的，是局部性质。因此一个函数在其整个定义区间上可能有多个极大值或极小值，并对同一个函数来说，在某一点的极大值也可能小于另一点的极小值。例.判断下面4个命题，其中是真命题序号为。①可导函数必有极值；②函数在极值点必有定义；③函数的极小值一定小于极大值（设极小值、极大值都存在）；④函数的极小值（或极大值）不会多于一个。②xy2如例1求函数的极值。314xx31y3x(-∞，-2）-2(-2，2）2(2，+∞）y′y解：定义域为R，y′=x2-4由y′=0可得x=-2或x=2当x变化时，y′,y的变化情况如下表：因此，当x=-2时，y极大值=17/3当x=2时，y极小值=－5++0-0极大值17/3极小值-5求可导函数f(x)极值的步骤：(2)求导数f’(x)；(3)求方程f’(x）=0的根；(4)把定义域划分为部分区间，并列成表格检查f’(x)在方程根左右的符号——•如果左正右负（+~-），那么f(x)在这个根处取得极大值；•如果左负右正（-~+），那么f(x)在这个根处取得极小值；(1)确定函数的定义域；例2求函数y=(x2-1)3+1的极值。x(-∞,-1)-1(-1,0)0(0,1)1(1,+∞)y′－0－0+0+y解：定义域为R，y′=6x(x2-1)2。由y′=0可得x1=-1,x2=0，x3=1当x变化时，y′,y的变化情况如下表：因此，当x=0时，y极小值=0无极值无极值极小值0例3已知函数f(x)=x3+ax2+bx+c，当x=-1时取得极大值7；当x=3时取得极小值，求这个极小值及a、b、c的值。函数在时有极值10，则a，b的值为（）A、或B、或C、D、以上都不对223)(abxaxxxf1x3,3ba11,4ba1,4ba11,4ba11,4baC，解:由题设条件得：0)1(10)1(/ff0231012baaba解之得11433baba或通过验证，都合要求，故应选择A。注意：f/(x0)=0是函数取得极值的必要不充分条件注意代入检验课堂练习32()fxaxbxcx2.(2006年北京卷)已知函数在点处取得极大值5,其导函数的图像(如图)过点（1,0）,（2,0）,求：（1）的值；（2）a,b,c的值；0x'()yfx0x2,9,12abc.10x)0(23(2/acbxaxxf）＝或－23332acab5)1(...