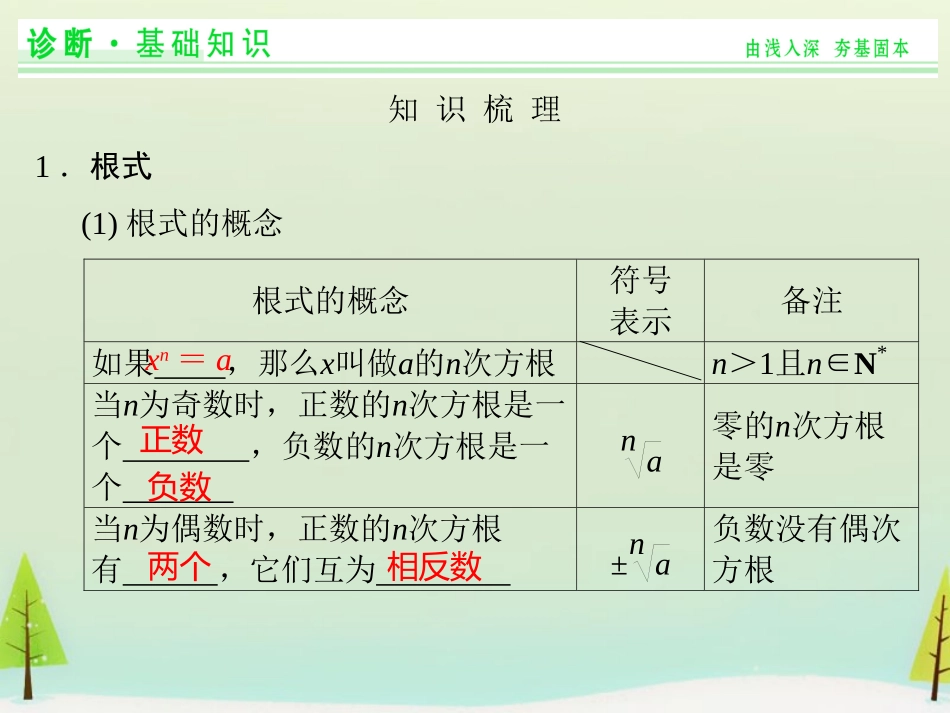
第5讲指数与指数函数知识梳理1.根式(1)根式的概念根式的概念符号表示备注如果,那么x叫做a的n次方根n>1且n∈N*当n为奇数时,正数的n次方根是一个,负数的n次方根是一个na零的n次方根是零当n为偶数时,正数的n次方根有,它们互为±na负数没有偶次方根xn=a正数负数两个相反数(2)两个重要公式①nan=,n为奇数,|a|=,a≥0,-a,a<0,n为偶数.②(na)n=.aaa11apnam1nam0无意义(2)有理数指数幂的性质①aras=(a>0,r,s∈Q);②(ar)s=(a>0,r,s∈Q);③(ab)r=(a>0,b>0,r∈Q).ar+sarsarbr3.指数函数的图象与性质y=axa>10<a<1图象定义域.值域.性质过定点.当x>0时,;x<0时,.当x>0时,;x<0时,.在(-∞,+∞)上是.在(-∞,+∞)上是.(0,+∞)R(0,1)y>10<y<10<y<1y>1增减函数函数辨析感悟1.指数幂的应用辨析(1)(4-2)4=-2.(×)(2)(教材探究改编)(nan)=a.(×)2.对指数函数的理解(3)函数y=3·2x是指数函数.(×)(4)y=1ax是R上的减函数.(×)(5)指数函数在同一直角坐标系中的图象的相对位置与底数的大小关系如图,无论在y轴的左侧还是右侧图象从上到下相应的底数由大变小.(×)(6)(2013·金华调研)已知函数f(x)=4+ax-1(a>0且a≠1)的图象恒过定点P,则点P的坐标是(1,5).(√)[感悟·提升]1.“nan”与“nan”的区别当n为奇数时,或当n为偶数且a≥0时,nan=a,当n为偶数,且a<0时,nan=-a,而(na)n=a恒成立.如(1)中4-2不成立,(2)中6-22=32≠3-2.2.两点注意一是指数函数的单调性是底数a的大小决定的,因此解题时通常对底数a按0<a<1和a>1进行分类讨论,如(4);二是指数函数在同一直角坐标系中的图象与底数的大小关系,在y轴右侧,图象从上到下相应的底数由大变小,在y轴左侧,图象从上到下相应的底数由小变大.如(5).规律方法进行指数幂运算时,一般化负指数为正指数,化根式为分数指数幂,化小数为分数,同时兼顾运算的顺序.需注意下列问题:(1)对于含有字母的化简求值的结果,一般用分数指数幂的形式表示;(2)应用平方差、完全平方公式及apa-p=1(a≠0)简化运算.答案-9a考点二指数函数的图象及其应用【例2】(1)(2014·泰安一模)函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是________.①a>1,b<0;②a>1,b>0;③0<a<1,b>0;④0<a<1,b<0.(2)比较下列各式大小.①1.72.5______1.73;②0.6-1______0.62;③0.8-0.1______1.250.2;④1.70.3______0.93.1.解析(1)由f(x)=ax-b的图象可以观察出,函数f(x)=ax-b在定义域上单调递减,所以0<a<1.函数f(x)=ax-b的图象是在f(x)=ax的基础上向左平移得到的,所以b<0.(2)①, 函数y=1.7x是增函数,2.5<3,∴1.72.5<1.73.② y=0.6x是减函数,-1<2,∴0.6-1>0.62.③ (0.8)-1=1.25,∴问题转化为比较1.250.1与1.250.2的大小. y=1.25x是增函数,0.1<0.2,∴1.250.1<1.250.2,即0.8-0.1<1.250.2.④ 1.70.3>1,0.93.1<1,∴1.70.3>0.93.1.答案(1)④(2)①<②>③<④>规律方法(1)对指数型函数的图象与性质(单调性、最值、大小比较、零点等)的求解往往利用相应指数函数的图象,通过平移、对称变换得到其图象,然后数形结合使问题得解.(2)一些指数方程、不等式问题的求解,往往利用相应指数型函数图象数形结合求解.【训练2】已知实数a,b满足等式2011a=2012b,下列五个关系式:①0<b<a;②a<b<0;③0<a<b;④b<a<0;⑤a=b.其中不可能成立的关系式有________.解析设2011a=2012b=t,如图所示,由函数图象,可得(1)若t>1,则有a>b>0;'(2)若t=1,则有a=b=0;(3)若0<t<1,则有a<b<0.故①②⑤可能成立,而③④不可能成立.答案③④考点三指数函数的性质及其应用【例3】已知函数f(x)=12x-1+12x3.(1)求函数f(x)的定义域;(2)讨论f(x)的奇偶性;(3)求证:f(x)>0.审题路线由2x-1≠0可求f(x)的定义域⇒分别求g(x)=12x-1+12与h(x)=x3的奇偶性⇒可利用g(-x)±g(x)=0判断g(x)的奇偶性⇒利用“奇×奇=偶,奇×偶=奇”判断f(x)的奇偶性⇒先证...