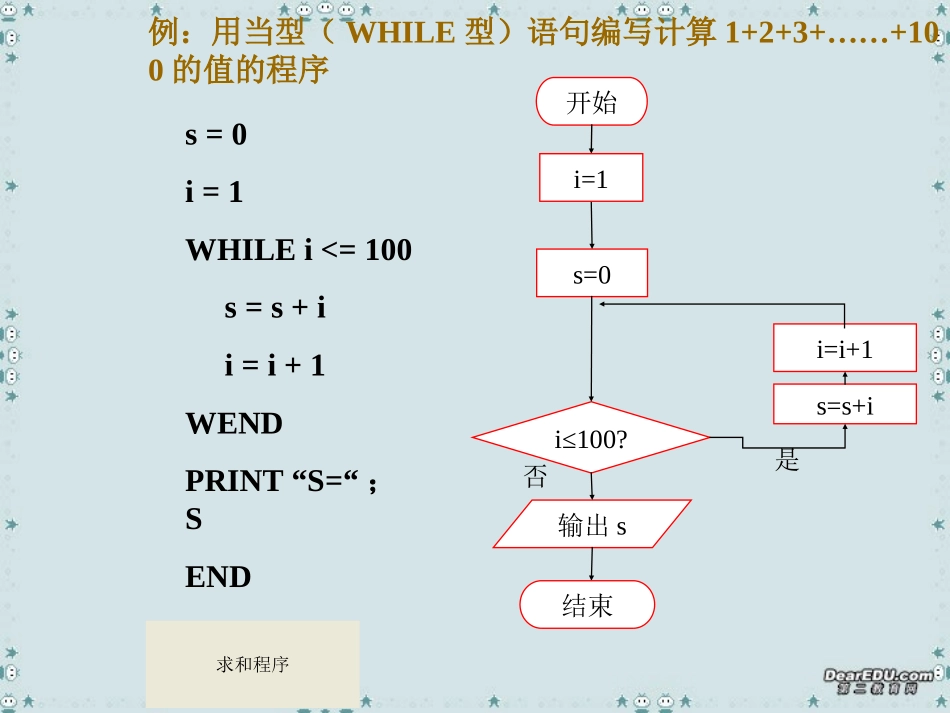
第一章算法初步1.1算法与程序框图1.2基本算法语句1.3算法案例一、循环语句作用:用来实现算法循环结构的功能。格式一当型(while型):1.2.3循环语句满足条件?是否循环体WHILE条件循环体WENDs=0i=1WHILEi<=100s=s+ii=i+1WENDPRINT“S=“;SEND求和程序例:用当型(WHILE型)语句编写计算1+2+3+……+100的值的程序开始s=0i=i+1s=s+ii≤100?输出s否是i=1结束格式二直到型(until型):DO循环体LOOPUNTIL条件循环体满足条件?否否是开始s=0i=i+1s=s+ii>100?输出sum结束否是求和程序例:用直到型(until型)语句编写计算1+2+3+……+100的值的程序i=1s=0i=1DOs=s+ii=i+1LOOPUNTILi>100PRINT“S=“;SEND综合应用例子:判断质数程序算法分析:第一步:判断n是否等于2。若n=2,则n是质数;若n>2,则执行第二步。第二步:依次从2~(n-1)检验是不是n的因数,即整除n的数,若有这样的数,则n不是质数;若没有这样的数,则n是质数。例1、任意给定一个大于1的整数n,试设计出一个程序或步骤对n是否为质数做出判定开始输入ni=2求n除以i的余数i=i+1i>=n或r=0?r=0?n不是质数n是质数结束是是是否判断质数程序否INPUT“n=“;ni=2DOr=nMODIi=i+1LOOPUNTILi>=nORr=0IFr=0THENPRINT“nisnotaprimenumber.”ELSEPRINT“nisaprimenmber.”ENDIFEND程序:二、条件语句的应用实例例5、编写程序,输入一个一元二次方程ax^2+bx+c=0的系数,输出它的实数根。开始输入a,b,cΔ=b-4acp=-b/(2a)q=SQR(ABS(Δ)/(2a))x1=p+qx2=p-qΔ≥0x1=x2?原方程有两个不等的实数根x1、x2原方程有两个相等的实数根x1、x2原方程无实数根结束是否是否求一元二次方程实数根求一元二次方程的根INPUT“a,b,c=“;a,b,cd=b*b-4*a*cIFd>=0THENp=-b/(2*a)q=SQR(d)/(2*a)IFd=0THENPRINT“Onerealroot:”;pELSEx1=p+qx2=p-qPRINT“Tworealroots:”;x1,x2ENDIFELSEPRINT“Norealroot.”ENDIFEND二、条件语句的应用实例例6、编写程序,使得任意输入的3个整数按从大到小的顺序输出。算法分析:(设a》b》c)第一步:输入3个整数a,b,c。第二步:将a与b比较,并把小的赋给b,大的赋给a。第三步:将a与c比较,并把小的赋给c,大的赋给a,此时a已是三个当中最大的。第四步:将b与c比较,并把小的赋给c,大的赋给b,此时a,b,c已按从小到大的顺序排列好。第五步:按顺序输出a,b,c。INPUT“a,b,c=“;a,b,cIFb>aTHENt=aa=bb=tENDIFIFc>aTHENt=aa=cc=tENDIFIFc>bTHENt=bb=cc=tENDIFPRINTa,b,cEND开始t=a,a=b,b=tt=a,a=c,c=tt=b,b=c,c=t输入a,b,c输入a,b,cb>a?c>a?c>b?结束是是否否是否计算程序三、课后练习p.24练习第一题程序p.24练习第二题程序p.24练习第三题程序三、课后练习1:二分法求平方根开始a=1b=2f(x)=x2-3a=mb=mm=(a+b)/2a=mb=mf(m)=0f(x1)f(m)>0|a-b|<0.005结束输出所求的近似根mm=(a+b)/2ynnyny三、课后练习2:程序:x=1y=0DOy=x^2-3*x+5PRINT“x=”;x,”y=“;yx=x+1LOOPUNTILx>20END三、课后练习3:INPUT“n=“;ni=1f=1WHILEi<=nf=f*Ii=i+1WENDPRINTfEND