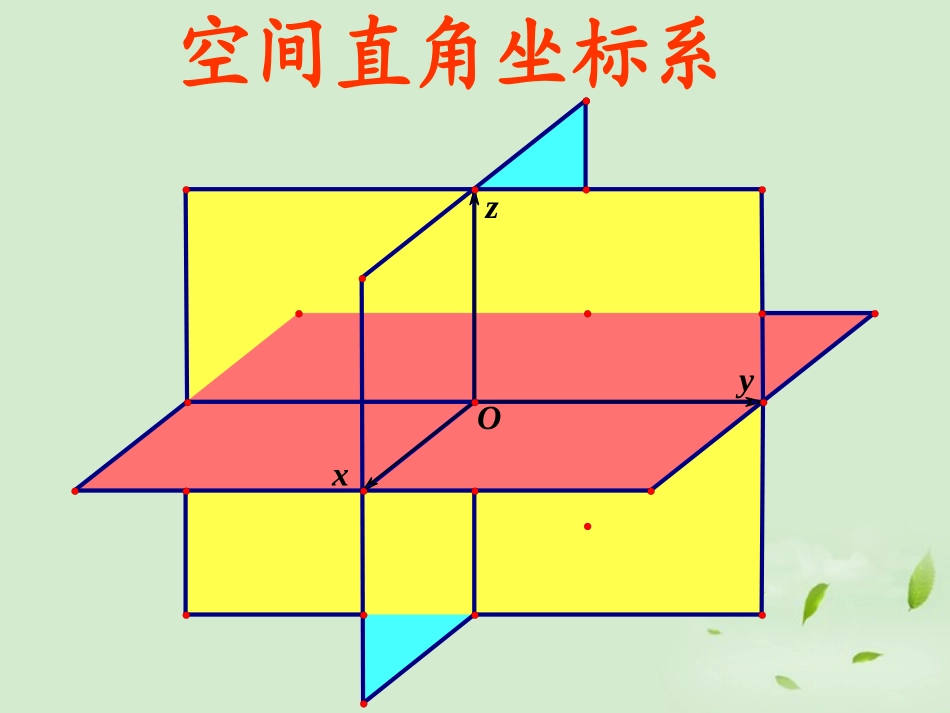
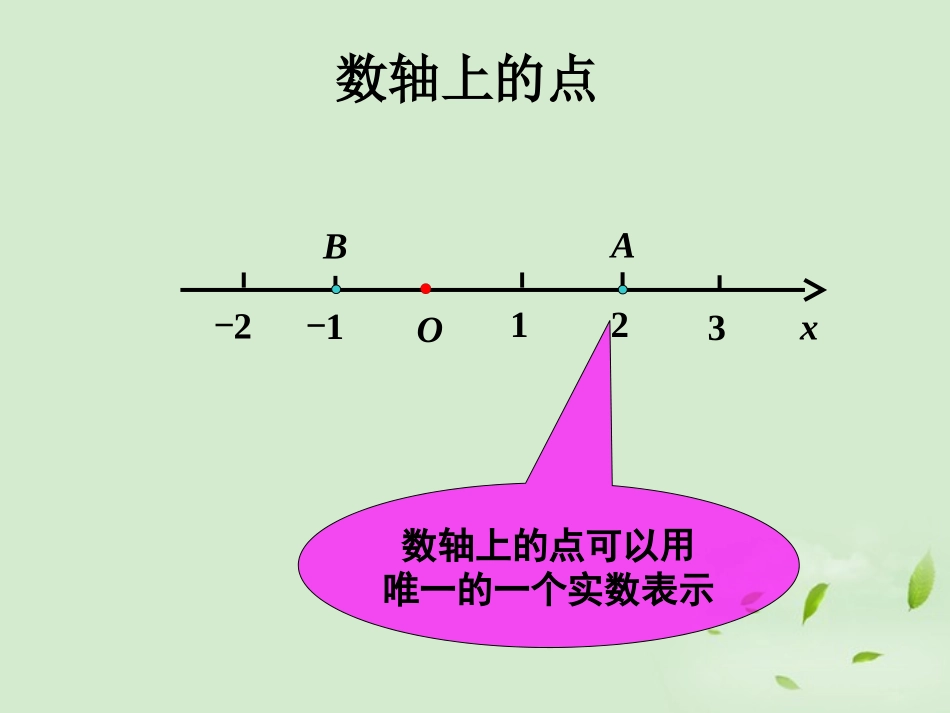
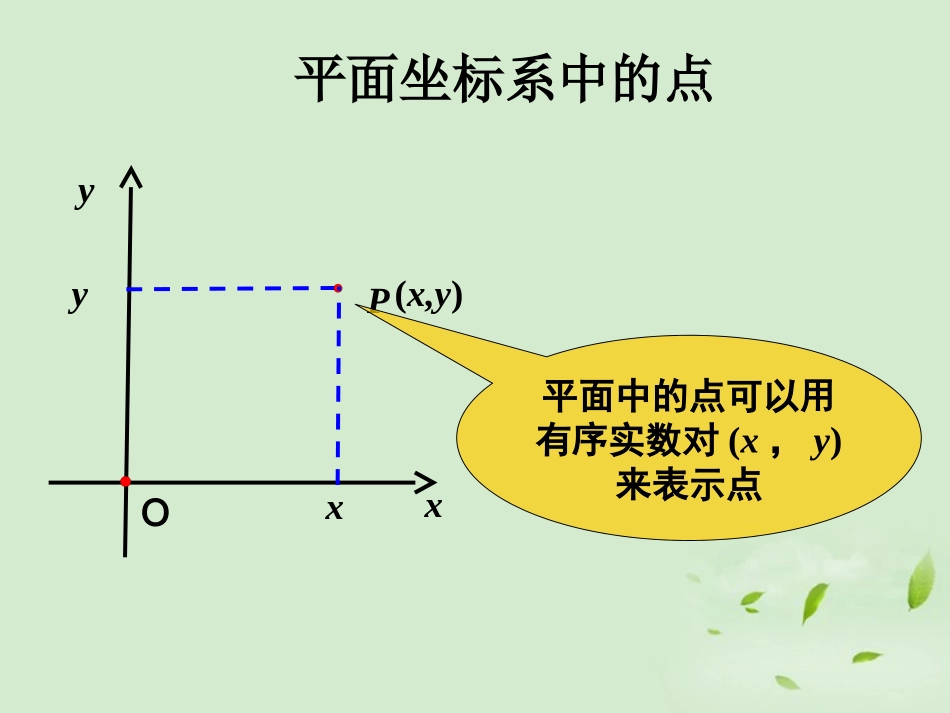
xOzy空间直角坐标系xO数轴上的点可以用唯一的一个实数表示-1-2123AB数轴上的点xyPOxy(x,y)平面中的点可以用有序实数对(x,y)来表示点平面坐标系中的点yOx在教室里同学们的位置坐标讲台yOx教室里某位同学的头所在的位置z如何确定空中飞行的飞机的位置?xo右手直角坐标系空间直角坐标系yz—Oxyz横轴纵轴竖轴111Ⅶxyozxoy面yoz面zox面空间直角坐标系共有八个卦限ⅠⅡⅢⅣⅤⅥⅧ点的坐标:x称为点P的横坐标OxyzPxPzxzyPPyy称为点P的纵坐标z称为点P的竖坐标反之:(x,y,z)对应唯一的点P空间的点P有序数组),,(zyx11C'D'B'A'COAByzxxoy平面上的点竖坐标为0yoz平面上的点横坐标为0xoz平面上的点纵坐标为0x轴上的点纵坐标竖坐标为0z轴上的点横坐标纵坐标为0y轴上的点横坐标竖坐标为0一、坐标平面内的点二、坐标轴上的点xyzo(3,4,2)(3,0,0)(0,4,0)(0,0,2)(3,4,0)3AB'A'D'B'C2C4例题例1、如下图,在长方体OABC-D`A`B`C`中,|OA|=3,|OC|=4,|OD`|=2,写出D`,C,A`,B`四点的坐标.xyzo(3,4,3)(0,4,0)3AB'A'D'B'C3C41.52P(1.5,2,3)练习11、如下图,在长方体、如下图,在长方体OABC-D`A`B`C`OABC-D`A`B`C`中,中,|OA|OA|=3|=3,,|OC|=4|OC|=4,,|OD`|=3|OD`|=3,,A`C`A`C`于于B`D`B`D`相交相交于点于点P.P.分别写出点分别写出点CC,,B`B`,,PP的坐标的坐标..练习zxyABCOA`D`C`B`QQ`22、如图,棱长为、如图,棱长为aa的正方体的正方体OABC-D`A`B`C`OABC-D`A`B`C`中,中,对角线对角线OB`OB`于于BD`BD`相交于点相交于点Q.Q.顶点顶点OO为坐标原点,为坐标原点,OAOA,,OCOC分别在分别在xx轴、轴、yy轴的正半轴上轴的正半轴上..试写出点试写出点QQ的坐标的坐标..结晶体的基本单位称为晶胞,如图是食盐晶胞示意图(可看成是八个棱长为1/2的小正方体堆积成的正方体),其中红色点代表钠原子,黑点代表氯原子,如图:建立空间直角坐标系后,试写出全部钠原子所在位置的坐标。xyzO例2:yzxP135例2xoyz对称点xyOx0y0(x0,y0)P(x0,-y0)P1横坐标不变,纵坐标相反。(-x0,y0)P2横坐标相反,纵坐标不变。P3横坐标相反,纵坐标相反。-y0-x0(-x0,-y0)空间对称点xoyz1(1,1,1)P(1,1,1)P2(1,1,1)P3(1,1,1)P点M(x,y,z)是空间直角坐标系Oxyz中的一点,写出满足下列条件的点的坐标(1)与点M关于x轴对称的点(2)与点M关于y轴对称的点(3)与点M关于z轴对称的点(4)与点M关于原点对称的点(5)与点M关于xOy平面对称的点(6)与点M关于xOz平面对称的点(7)与点M关于yOz平面对称的点(x,-y,-z)(-x,y,-z)(-x,-y,z)(-x,-y,-z)(x,y,-z)(x,-y,z)(-x,y,z)关于谁对称谁不变xyzo空间点到原点的距离ABC(,,)Pxyz||||BPz22||OBxy222||OPxyz空间两点间的距离公式22121212||()()PPxxyy平面:类比猜想22212121212||()()()PPxxyyzz空间:例3求证以)1,3,4(1M、)2,1,7(2M、)3,2,5(3M三点为顶点的三角形是一个等腰三角形.解221MM,14)12()31()47(222232MM,6)23()12()75(222213MM,6)31()23()54(22232MM,13MM原结论成立.例4已知A(-3,2,1)、B(0,2,5).△AOB的周长.解由两点间距离公式可得,5)51()22()03(222BA由两点间距离公式可得,1412)3(222OA.29520222BO所以,△AOB的周长.1429145BOAOABl例5设P在x轴上,它到)3,2,0(1P的距离为到点)1,1,0(2P的距离的两倍,求点P的坐标.解设P点坐标为),0,0,(x因为P在x轴上,1PP22232x,112x2PP22211x,22x1PP,22PP112x222x,1x所求点为).0,0,1(),0,0,1(练习•P138练习1.(只求距离)(1)||6AB(2)||70AB一、空间直角坐标系二、空间两点间的距离公式:(注意它与平面直角坐标系的区别)(轴、面、卦限)小结21221221221zzyyxxPP三、空间两点间的中点坐标公式:)2zz,2yy,2xx()z,y,x(M212121