高二数学课件二项式定理应用复习课 课件VIP免费

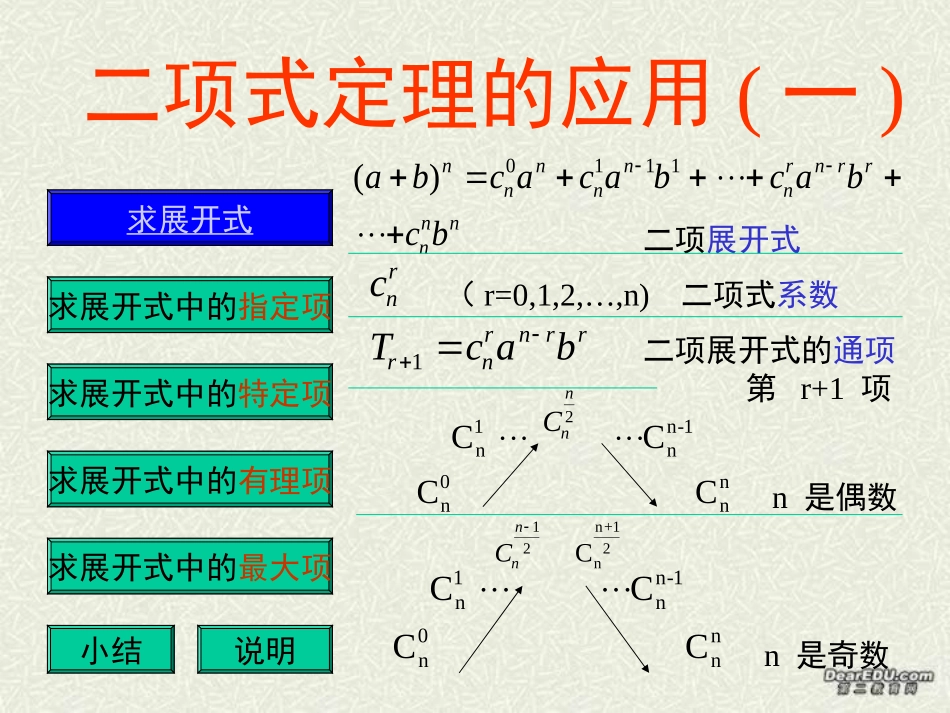
多媒体二项式定理的应用(一)求展开式求展开式中的指定项求展开式中的特定项求展开式中的有理项求展开式中的最大项小结说明()abcacabcabcbnnnnnnrnrrnnn0111二项展开式cnr（r=0,1,2,…,n)二项式系数Tcabrnrnrr1二项展开式的通项第r+1项Cnn2Cnn12Cnn+12CCCCn1nn-1n0nnCCCCn1nn-1n0nnn是偶数n是奇数问题1问题2求的展开式(1-x)5()125xx用关于的次多项式表示().rnrn1退出求的展开式(1-x)5()125xx分析：由知，原式可变形为再展开，比直接展开简便。ababnnn()()135x解：()()()11115101055253550513526539541255153691215xxxxccxcxcxcxcxxxxxx退出用关于的次多项式表示().rnrn1分析：若把表示为运用二项式定理，就可得到所求的表达式。rn[()]rn11解：rrnn[()]11=c(r-1)+c(r-1)+c(r-1)++cn0nn1n-1n2n-2nn退出问题3求的展开式中第四项的二项式系数和第四项的系数().xx210退出求的展开式中第四项的二项式系数和第四项的系数().xx210分析：第k+1项的二项式系数----------第k+1项的系数--------------------具体数值的积。cnk解：因为所以第四项的二项式系数是第四项的系数是TTcxxc431310373103121208960()()(),..-c103退出问题4退出求展开式中的常数项().91318xx求展开式中的常数项().91318xx分析：常数项是含的项，即不含x的项。x0解：TCxxCxkkkkkkkkkk118183181818321911913()()()()令则183201291318564131211812612186kkTTCC,..退出问题5退出求的展开式中有多少项有理项().573100项求的展开式中有多少项有理().573100解：由知均为整数时为有理数为的倍数且即为展开式中共有项有理项TCkkTkkkkkkk11001002357100236010006129617(),,.,.,,,,,.退出问题6退出设问在的展开式中最大的项是第几项xx5115,(),?设问在的展开式中最大的项是第几项xx5115,(),?退出分析：.T,TTTTrrrrr最大时且当11解：因此最大项是第14项得由111515111515rrrrrrrrxCxCxCxCrrrr161515151340337r解得13r利用二项式定理和通项公式及二项式系数的性质，解决问题时，需熟练地掌握公式并灵活地变换，同时要综合运用各种数学知识。退出作业本10.