高一数学同角三角函数的基本关系式 课件VIP免费

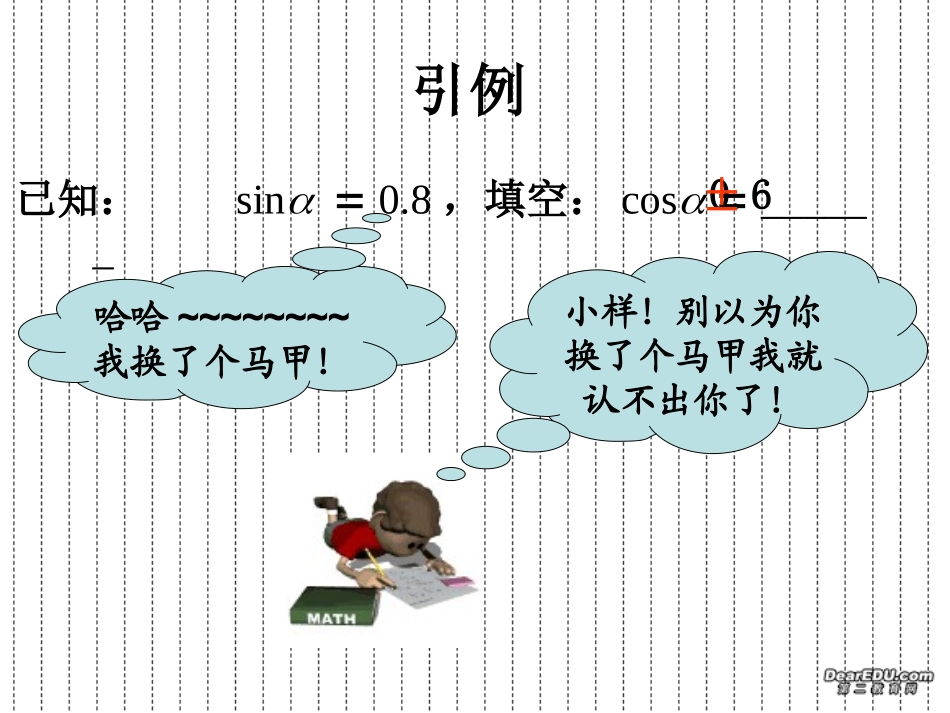
同角三角函数的基本关系式本节知识在整章的地位第四章三角函数与三角函数相关的几个基本概念三角公式三角函数的图象与性质三角式的恒等变形诱导公式同角三角函数的基本关系式和差角公式，倍角公式，等变角、变名、变结构角不变，变名、变结构引例已知：sin0.8，填空：cos______哈哈~~~~~~~~我换了个马甲！小样！别以为你换了个马甲我就认不出你了！0.6±复习：三角函数的符号已知：sin0.8，填空：cos______±0.6xyOsin、csc、、、、＋＋xyOcos、sec、、、、＋＋xyOtan、cot、、、、－－－－＋－＋－已知：sin0.8，填空：cos______在初中，我们学过以下三个三角公式：22sincos1sintancostancot1在初中，公式中的角为锐角！对任意角这些公式是否成立？±0.6还需重新证明！波利亚：“回到定义去！”正弦sin余弦cos正切tan余割csc正割sec余切cotP(x，y)xyOryrxryxxyrxry22rxy其中：、、、、=1、、、、=1、、、、=1同角三角函数的倒数关系正弦sin余弦cos正切tan余割csc正割sec余切cot22rxy其中：···P(x，y)xyOrsintancosyyrxxr平方关系和商数关系sin2cos2sin2cos2yrxr y2x2r2，∴sin2cos2R22rxyP(x，y)xyOr2kkZ，sincostanyrxryx；；；cotseccscxyrxry；；．同角三角函数的基本关系式平方关系：22sincos1，sintancos，tancot1，商数关系：倒数关系：cossec1，sincsc1，学习数学公式需要做好哪几件事？第一件事：记住它！学习数学公式需要做好哪几件事？•记住它！（通过分析式子的结构来记忆）•明确公式成立的条件（何时“不必疑”？）公式成立的条件平方关系：22sincos1，sintancos，tancot1，商数关系：倒数关系：cossec1，sincsc1，R(Z)2kk(Z)2kk(Z)2kk(Z)kk两边都有意义约定：（详见课本第24页倒数第5行）学习数学公式需要做好哪几件事？•记住它！（通过分析式子的结构来记忆）•明确公式成立的条件（何时“不必疑”？）•熟悉公式的变形（换马甲）游戏：判断对错•1•2•3•4•5•62cos1sin±sincostancoscotsin221tan+1cossin2cos2122sin27+cos631cos(30)sin(30)cot(30)xxx27学习数学公式需要做好哪几件事？•记住它！（通过分析式子的结构来记忆）•明确公式成立的条件（何时“不必疑”？）•熟悉公式的变形（换马甲）•熟悉公式的一些典型应用•熟悉应用公式时的易错点公式运用三类题型•已知一个角的一个三角函数值，求这个角的其它几个三角函数值。•三角函数式的化简•三角恒等式的证明下节课再讲公式运用之一已知一个角的一个三角函数值，求这个角的其它几个三角函数值。sincostansec倒数关系cot倒数关系csc倒数关系公式运用之一已知一个角的一个三角函数值，求这个角的其它几个三角函数值。sincostansintancos公式运用之一已知一个角的一个三角函数值，求这个角的其它几个三角函数值。sincostan22sincos1例题（一）例1已知：sin0.8，且为第三象限角，求：cos，tan，cot、、.解： 为第三象限角，∴cos<0，于是2cos1sin0.6从而sin4tancos313cottan4解： cosm0，1，∴为第一、四象限角,当为第一象限角时，sin>0，于是例题（二）例2已知：cosm，且m0，1，求tan．22sin1cos1m从而2sin1tancosmm当为第四象限角时，同理可得：21tanmm不打草稿，你能否找出其中的错误？sintancos公式运用之一已知一个角的一个三角函数值，求这个角的其它几个三角函数值。sincostan22sincos1??例题（二）...