高一数学三角函数的图象与性质 苏教版 课件VIP免费

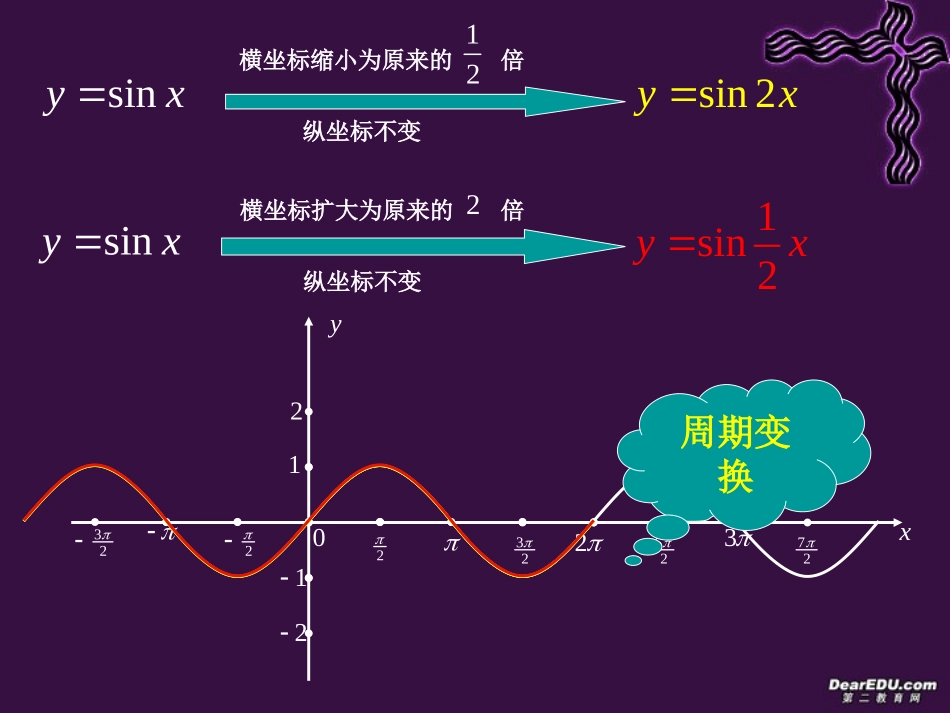
三角函数的图象与性质高一数学备课组一般地，函数sin(),yAxxR及函数cos(),yAxxR（其中,,A为常数，且0,0A）的周期2TA频率：12fT振幅：相位：x时的相位0x称为初相sinyxsin2yxsinyx1sin2yx纵坐标不变横坐标缩小为原来的倍12纵坐标不变横坐标扩大为原来的倍2xy02322523722321212周期变换sinyx2sinyx横坐标不变纵坐标扩大为原来的倍2sinyx1sin2yx横坐标不变纵坐标缩小为原来的倍12xy02322523722321212振幅变换sinyxsin()3yx向左平移单位3sinyxsin()3yx向右平移单位3xy02322523722321212相位变换sinyxsinyxxy02322523722321212sinyx的最小正周期是1sin2yx的最小正周期是sinyxsinyxxy02322523722321212sinyx的周期是不具有周期性xy02322523722321212sinyxsin2yx3sinyxsin2yxxy02322523722321212sin(2)3yxsin()3yx213cossincos1()22yxxxxR例2.已知函数该函数的图象可由sin()yxxR的图象经过怎样的平移和伸缩变换得到.解:1cos213sin21224xyx1135(cos2sin2)2224xx15(sincos2cossin2)2664xx15sin(2)264x将函数sinyx作如下变换在求周期，单调区间，最值以及图象变换等问题，sin()yAx一般情况下都要把所给函数转化成213cossincos1()22yxxxxR函数周期是sinyxsin()6yx1sin(2)26yxsin(2)6yxsin2yx15sin(2)264yx图象向左移个单位6图象向左移个单位12纵坐标不变,横坐标缩小为原来的倍12纵坐标不变,横坐标缩小为原来的倍12横坐标不变,纵坐标缩小为原来的倍12图象向上平移单位54例3.已知函数()yfx的图象右移8个单位,然后再把图象上每一点的横坐标扩大为原来的两倍,所得的图象恰好与函数3sin()6yx的图象相同,求()fx的解析式.解：3sin(2)6yx①将3sin()6yx图象上每一点的横坐标缩小为原来的一半（纵坐标不变）得到函数的图象②将所得的图象向左平移8个单位得：3sin[2()]86yx整理得：53sin(2)12yx例１．已知正弦函数sin()(0,0)yAxA（１）求此函数的解析式1();fx（２）求与1()fx图象关于直线8x对称的曲线解析式2();fx（３）作出函数12()()yfxfx的图象的简图xy02468102228x解：由图象可知，2,A216,T即8将2,2xy代入，得22sin(2)8即sin()14解得41()2sin()84fxx求常用以下两种方法：（１）利用已知点坐标（最高点，最底点，零点）代入解析式，再结合图形求出（２）若能求出离原点最近的上升（或下降）的零点横坐标，则令或即可求0x0(0x0)x(2)设2()yfx上任一点为(,)xy其关于直线8x对称的点为''(,)xy则有''82xxyy即''16xxyy代入1()yfx得2sin[(16)]84yx2()2sin()84fxx(3)12()()yfxfx2sin()2sin()8484xx22cossin84x2cos8x8x02322x0481216cos8x101012cos8yx20202列表：xy0246810222121416练习题：sin()(0,0,0)yAxkA已知曲线在同一个周期内的最高点的坐标为(,4)8，最底点的坐标为5(,2)8求此曲线的函数表达式.xy02322523722321212xy02322523722321212xy02468102228x