高三数学函数的极限1 课件VIP免费

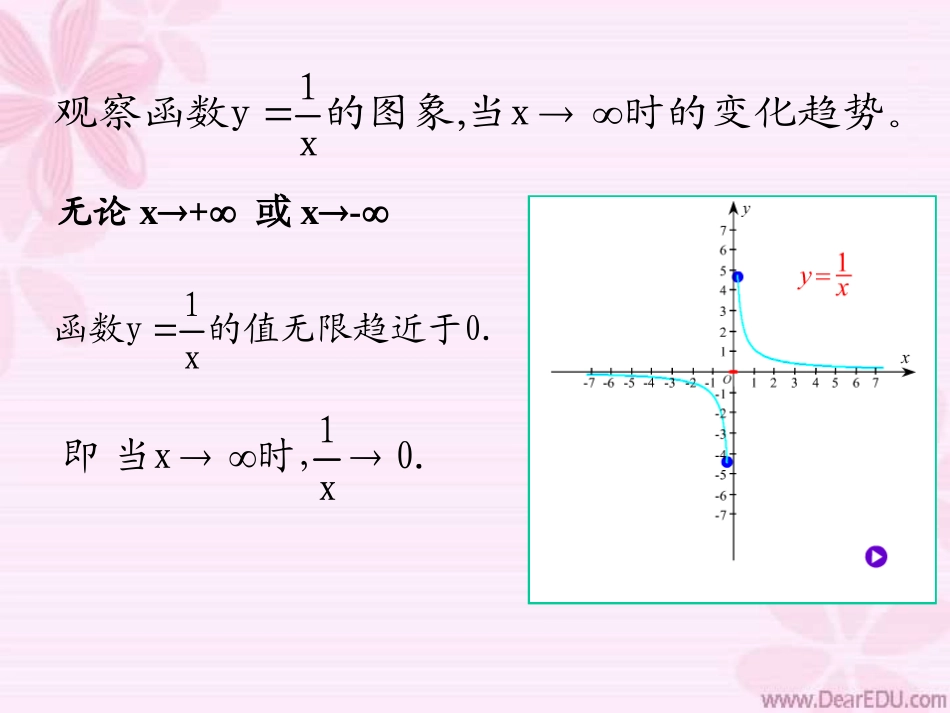
复习1、数列的极限：如果当项数n无限增大，数列的项an无限趋近于某个常数a（即|an-a|无限地接近于0），称数列{an}以a为极限。aannlim数列{an}以a为极限，记作2、常见数列的极限如：③当|a|<1时，则0limnna01limnn①)(lim为常数CCCn②3、数列与函数的关系：数列可以看作是定义在正整数集上的一种特殊函数。1观察函数y的图象,当x时的变化趋势。x无论x+或x-的值无限趋近于0.x1函数y0.x1时，当x即2.3函数的极限x110100100010000100000···y10.10.010.0010.00010.00001···考察函数当x无限增大时的变化趋势．xy1yxO当自变量x取正值并无限增大时，函数的值无限趋近于0，即|y-0|可以变得任意小．xy1当x趋向于正无穷大时，函数xy1的极限是0，记作01limxx2.3函数的极限yxOxy1当x趋向于负无穷大时，函数的极限是0，记作01limxx2.3函数的极限就说当x趋向于正无穷大时，函数的极限是a，记作axfx)(lim)(xf一般地，当自变量x取正值并且无限增大时，如果函数)(xf无限趋近于一个常数a，也可记作:当axfx)(时，当就说当x趋向于负无穷大时，函数的极限是a，记作axfx)(lim当自变量x取负值并且绝对值无限增大时，如果函数)(xf无限趋近于一个常数a，也可记作:axfx)(时，)(xf2.3函数的极限如果axfaxfxx)(lim)(lim且那就是说当x趋向于axfx)(lim也可记作:当axfx)(时，无穷大时，函数的极限是a，记作)(xfCxfx)(lim对于常数函数)()(RxCxf也有2.3函数的极限x取正值并且无限增大axfx)(lim无限趋近于常数a)(xf极限表示值的变化趋势自变量x的变化趋势)(xfx取负值并且绝对值无限增大axfx)(lim无限趋近于常数a)(xfx取正值并且无限增大，x取负值并且绝对值无限增大axfx)(lim无限趋近于常数a)(xf2.3函数的极限例1、分别就自变量x趋向于的情况，讨论下列函数的变化趋势：和（1）xy21解：当时，无限趋近于0，xy21;021limxx即x当时，趋近于.xy21x当时，都有1a00limxxa结论：2.3函数的极限（2）xy2当时，无限趋近于0，即xxy2;02limxx当时，趋近于.xy2x解：0limxxa当时，都有1a结论:2.3函数的极限（3）)0(1)0(0)0(1)(时时时xxxxf解：当时，的值保持为1．即x)(xf;1)(limxfx当时，的值保持为-1，即x)(xf;1)(limxfx解函数图象如右图所示，由图象可以看出：,1xxyx无论或函数+1的值无限趋近于1，(1)1x1所以lim.x例2、观察函数的图象，写出极限11xlimx11xy,2πarctanx时，y(1)当x2πarctanxlim即x解作函数y=arctanx的图象，由图象可以看出，,2πarctanx时，y(2)当x2πarctanxlim即xxxx此时，limarctanxlimarctanx所以，limarctanx不存在.例3、观察函数y=arctanx的图象。并写出xarctanlimx1xarctanlimx2课堂练习1.观察函数y=ex的图象，并写出xxelim)1(21)()1(xxf2.下列函数当x时极限是否存在，试说明理由，并画图观察。(2)f(x)=1xxelim)2(3.的值是()11lim22xxxA.0B.1C.不存在D.-10)21(limxx4.下列结论正确的是()A.B.C.D.0)31(limxx010limxx02limxxBD2.3函数的极限课堂小结本节学习了当x分别趋向于+∞,-∞,∞时，函数f(x)的极限，以及常数函数的极限，并且注意中的∞和数列极限中的∞不同意义，以概念为依据，结合函数图象，学会求一些函数的极限。)(limxfxnnalim