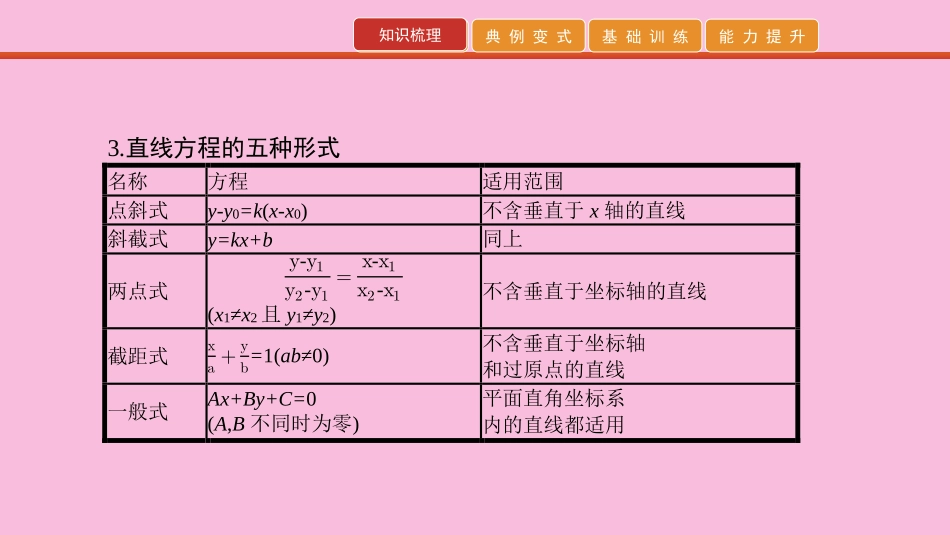
第26讲直线与方程知识梳理典例变式基础训练能力提升知识梳理1.直线的倾斜角定义:当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角;当直线l与x轴平行或重合时,规定它的倾斜角为0°.直线倾斜角的取值范围为0°≤α<180°.2.直线的斜率定义:当直线与x轴不垂直时,一条直线的倾斜角α的正切叫做这条直线的斜率,即k=tanα.α=90°,k不存在.公式:若P(x1,y1),P2(x2,y2)(x1≠x2),则k=𝑦2-𝑦1𝑥2-𝑥1.知识梳理典例变式基础训练能力提升知识梳理3.直线方程的五种形式名称方程适用范围点斜式y-y0=k(x-x0)不含垂直于x轴的直线斜截式y=kx+b同上两点式y-y1y2-y1=x-x1x2-x1(x1≠x2且y1≠y2)不含垂直于坐标轴的直线截距式xa+yb=1(ab≠0)不含垂直于坐标轴和过原点的直线一般式Ax+By+C=0(A,B不同时为零)平面直角坐标系内的直线都适用知识梳理典例变式基础训练能力提升知识梳理4.两条直线平行与垂直的判定(1)两条直线平行直线l1:y=k1x+b1l2:y=k2x+b2,则l1∥l2⇔k1=k2且b1≠b2,若k1、k2不存在时,l1与l2的关系为平行或重合.(2)两条直线垂直直线l1,l2的斜率分别为k1,k2,则l1⊥l2⇔k1k2=-1,若k1不存在,k2=0,则l1⊥l2.5.线段的中点坐标公式若P1(x1,y1),P2(x2,y2),线段P1P2的中点M(x,y),则ቄ𝑥=𝑥1+𝑥22,𝑦=𝑦1+𝑦22ቅ.知识梳理典例变式基础训练能力提升知识梳理6.两条直线相交直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的交点为M(x0,y0)⇔ቄ𝑥=𝑥0,𝑦=𝑦0为方程组൜𝐴1𝑥+𝐵1𝑦+𝐶1=0,𝐴2𝑥+𝐵2𝑦+𝐶2=0的解.l1与l2相交⇔方程组有唯一解,l1∥l2⇔方程组无解,l1与l2重合⇔方程组有无数组解.知识梳理典例变式基础训练能力提升知识梳理7.两个距离公式(1)平面上的两点P1(x1,y2),P2(x2,y2)间的距离公式|P1P2|=ට(𝑥2-𝑥1)2+(𝑦2-𝑦1)2,特别地,原点O(0,0)与任一点P(x,y)的距离|OP|=ඥ𝑥2+𝑦2.(2)点P0(x0,y0)到直线l:Ax+By+C=0的距离d=|𝐴𝑥0+𝐵𝑦0+𝐶|ට𝐴2+𝐵2.知识梳理典例变式基础训练能力提升典例变式题型一直线的倾斜角与斜率【例1】(1)(2019·石家庄模拟)直线x+(a2+1)y+1=0的倾斜角的取值范围是()A.ቂ0,π4ቃB.ቂ3π4,πቁC.ቂ0,π4ቃ∪ቀπ2,πቁD.ቂπ4,π2ቁ∪ቂ3π4,πቁ(2)直线l过点P(1,0),且与以A(2,1),B(0,ξ3)为端点的线段有公共点,则直线l斜率的取值范围为.知识梳理典例变式基础训练能力提升典例变式【解析】(1)由直线方程可得该直线的斜率为-1𝑎2+1,又-1≤-1𝑎2+1<0,所以倾斜角的取值范围是ቂ3π4,πቁ.(2)如图, kAP=1-02-1=1,kBP=ξ3-00-1=-ξ3,∴k∈(-∞,-ξ3]∪[1,+∞).【答案】(1)B(2)(-∞,-ξ3]∪[1,+∞)知识梳理典例变式基础训练能力提升典例变式【规律方法】(1)求倾斜角的取值范围的一般步骤:①求出斜率k=tanα的取值范围.②利用三角函数的单调性,借助图象,确定倾斜角α的取值范围.(2)斜率的求法:①定义法:若已知直线的倾斜角α或α的某种三角函数值,一般根据k=tanα求斜率.②公式法:若已知直线上两点A(x1,y1),B(x2,y2),一般根据斜率公式k=𝑦2-𝑦1𝑥2-𝑥1(x1≠x2)求斜率.知识梳理典例变式基础训练能力提升典例变式[注意]直线倾斜角的范围是[0,π),而这个区间不是正切函数的单调区间,因此根据斜率求倾斜角的范围时,要分ቂ0,π2ቁ,π2与ቀπ2,πቁ三种情况讨论.由正切函数图象可以看出,当倾斜角α∈ቂ0,π2ቁ时,斜率k∈[0,+∞);当α=π2时,斜率不存在;当α∈ቀπ2,πቁ时,斜率k∈(-∞,0).知识梳理典例变式基础训练能力提升典例变式变式训练一1.直线2xcosα-y-3=0ቀ𝛼∈ቂπ6,π3ቃቁ的倾斜角的变化范围是()A.ቂπ6,π3ቃB.ቂπ4,π3ቃC.ቂπ4,π2ቃD.ቂπ4,2π3ቃB【解析】直线2xcosα-y-3=0的斜率k=2cosα.由于α∈ቂπ6,π3ቃ,所以12≤cosα≤ξ32,因此k=2cosα∈[1,ξ3].设直线的倾斜角为θ,则有tanθ∈[1,ξ3].由于θ∈[0,π),所以θ∈ቂπ4,π3ቃ,即倾斜角的变化范围是ቂπ4,π3ቃ.知识梳理典例变式基础训练能力提升典例变式2.若点A(4,3),B(5,a),C(6,5)三点共线,则a的值为.4【解析】因为kAC=5-36-4=1,kAB=𝑎-35-4=a-3.由于A,B,C三点共线,所以a-3=1,即a=4.知识梳理典例变式基础训练能力提升典例变式3.已知三点A(a,2),B(3,7),C(-2,-9a)在一条直线上,...