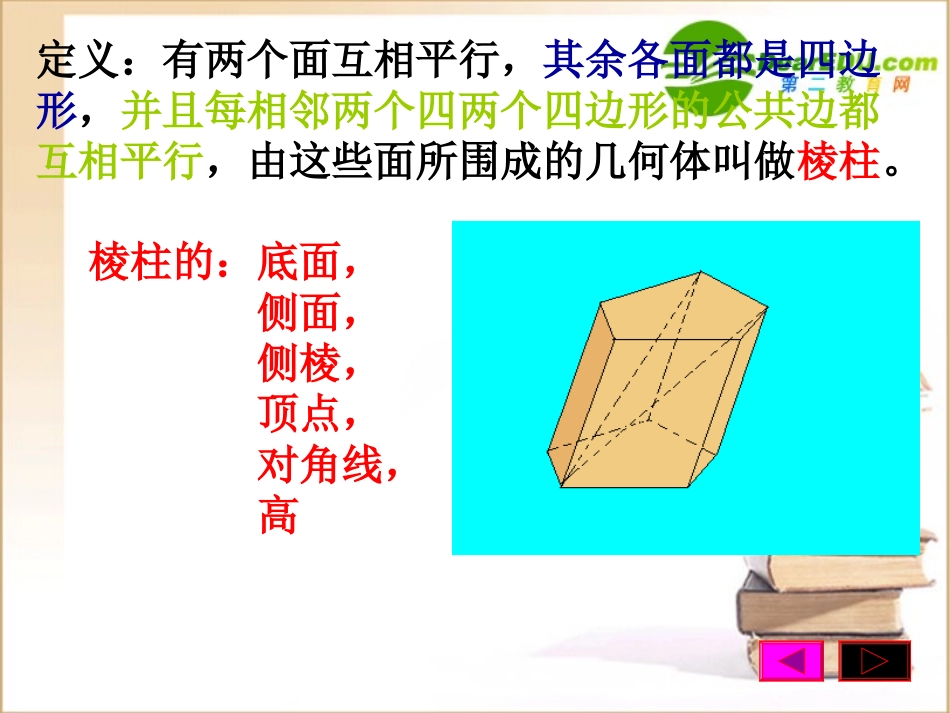
9.71、棱柱我们常见的一些物体,例如三棱镜,方砖以及螺杆的头部,它们都呈棱柱形状,如图:定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。棱柱的:底面,侧面,侧棱,顶点,对角线,高问题问题11::有两个面互相平行,其余各面都是四边形的几何体是棱柱吗?答:不一定是.如右图所示,不是棱柱.问题问题11::有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?答:不一定是.如右图所示,不是棱柱.棱柱的表示法;1.用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDE-A1B1C1D1E12.用表示一条对角线端点的两个字母表示,如:棱柱AC1ABCDA1A1A1B1B1B1C1C1C1D1D1E1ABCABCDE棱柱的底面可以是三角形、四边形、五边形、……我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……三棱柱四棱柱五棱柱1.侧棱不垂直于底的棱柱叫做斜棱柱。2.侧棱垂直于底的棱柱叫做直棱柱。3.底面是正多边形的直棱柱叫做正棱柱。棱柱的分类1按底面多边形的边数分类可分为三棱柱、四棱柱、五棱柱等等。.2.按侧棱与底面位置关系分类可分为斜棱柱、直棱柱、正棱柱。斜三棱柱直四棱柱正五棱柱练一练练一练练一练练一练面数最少的棱柱是棱柱。它有个面,其中个底面、个侧面,它有条棱,其中条侧棱,它有个顶点,条对角线N(N是正整数)棱柱有个面,其中个底面、个侧面,有条棱,其中条侧棱,有个顶点,条对角线ABCC1A1B1三5239360N+2N23NN2NN(N-3)棱柱的性质;1.侧棱都相等,侧面是平行四边形;2.两个底面与平行于底面的截面是全等的多边形;3.过不相邻的两条侧棱的截面是平行四边形。侧棱都相等,侧面是平行四边形已知:三棱柱ABC-A1B1C1求证:AA1=BB1=CC1,侧面ABB1A1是平行四边形证明:底面ABC∥底面A1B1C1底面ABC∩平面ABB1A1=AB底面A1B1C1∩平面ABB1A1=A1B1AB∥A1B1AA1∥B1B}侧面ABB1A1是平行四边形ABCC1A1B1}两个底面与平行与底面的截面是全等的多边形ABCC1B1MN已知:三棱柱ABC-A1B1C1,平面MNP∥底面ABC,且交三条侧棱于M、N、P求证:△MNPABC≌△平面MNP∥底面ABC平面MNP∩平面ABB1A1=MN平面ABC∩平面ABB1A1=AB证明:}MN∥ABAA1∥B1B}AMNBAB=MN同理:BC=NP,AC=MPA1P所以△MNPABC(SSS)≌△过不相邻的两条侧棱的截面是平行四边形ABCA1B1C1D1D已知:四棱柱ABCD-A1B1C1D1求证:截面AA1C1C是平行四边形证明:四棱柱ABCD-A1B1C1D1AA1∥C1C=截面AA1C1C是平行四边形1.有一个侧面是矩形的棱柱是不是直棱柱?有两个相邻侧面是矩形的棱柱呢?为什么?ABCA1B1C1分析:右图:AA1AB⊥且AA1与底面不垂直时,棱柱为斜棱柱。左图:两个相邻侧面与底面垂时,它们的交线也与底面垂直。2.斜棱柱、直棱柱和正棱柱的底面、侧面各有什么特点?1.斜棱柱、直棱柱的底面为任意多边形。正棱柱的底面为正多边形。2.斜棱柱的侧面为平行四边形。直棱柱的侧面为矩形。正棱柱的各个侧面为全等的矩形。3.棱柱集合、斜棱柱集合、直棱柱集合、正棱柱集合之间存在怎样的包含关系?棱柱集合斜棱柱集合直棱柱集合正棱柱集合4.正四棱柱中,求AC1与DC所成角的取值范围。ABCDA1B1C1D1总结:本节课主要学习了棱柱的定义及棱柱的有关性质:1.棱柱定义:棱柱的底面、侧面、侧棱、顶点、对角线、高。2.棱柱的性质;1.)侧棱都相等,侧面是平行四边形;2).两个底面与平行于底面的截面是全等的多边形;3.)过不相邻的两条侧棱的截面是平行四边形。