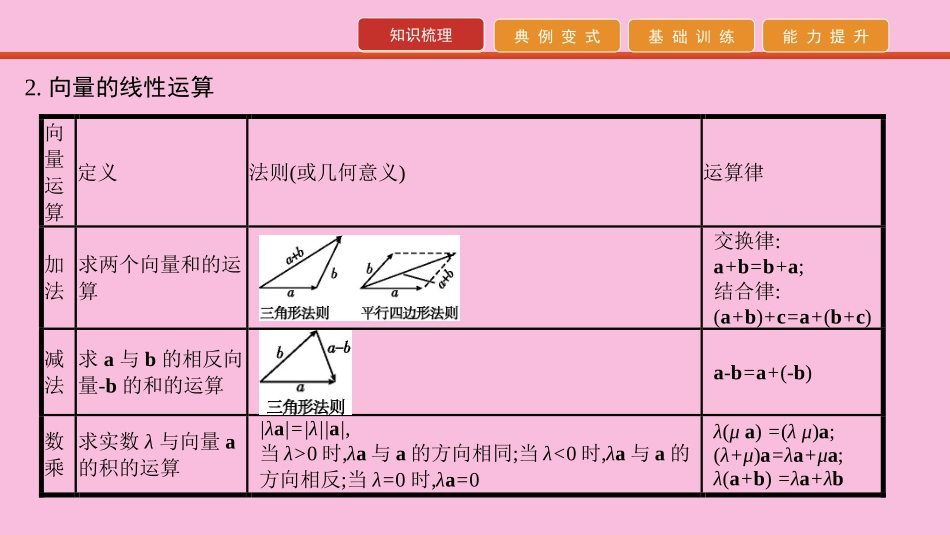
知识梳理典例变式基础训练能力提升第4讲平面向量的线性运算及基本定理知识梳理典例变式基础训练能力提升知识梳理1.平面向量的有关概念名称定义备注向量既有大小又有方向的量叫做向量;向量的大小叫做向量的长度(或称模)平面向量是自由向量,平面向量可自由平移零向量长度为0的向量;其方向是任意的记作0单位向量长度等于1个单位的向量非零向量a的单位向量为±𝑎|𝑎|平行向量方向相同或相反的非零向量,又叫做共线向量0与任一向量平行或共线相等向量长度相等且方向相同的向量两向量只有相等或不等,不能比较大小相反向量长度相等且方向相反的向量0的相反向量为0知识梳理典例变式基础训练能力提升知识梳理2.向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算交换律:a+b=b+a;结合律:(a+b)+c=a+(b+c)减法求a与b的相反向量-b的和的运算a-b=a+(-b)数乘求实数λ与向量a的积的运算|λa|=|λ||a|,当λ>0时,λa与a的方向相同;当λ<0时,λa与a的方向相反;当λ=0时,λa=0λ(μa)=(λμ)a;(λ+μ)a=λa+μa;λ(a+b)=λa+λb知识梳理典例变式基础训练能力提升知识梳理3.平面向量共线定理向量b与a(a≠0)共线的充要条件是有且只有一个实数λ,使得b=λa.4.平面向量基本定理如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.其中,不共线的向量e1,e2叫做表示这一平面内所有向量的一组基底.5.向量的夹角(1)定义:已知两个非零向量a和b,作𝑂𝐴ሬሬሬሬሬԦ=e,𝑂𝐵ሬሬሬሬሬԦ=b,则∠AOB就是向量a与b的夹角.(2)范围:设θ是向量a与b的夹角,则0°≤θ≤180°.(3)共线与垂直:若θ=0°,则a与b同向;若θ=180°,则a与b反向;若θ=90°,则a与b垂直.知识梳理典例变式基础训练能力提升典例变式题型一向量的线性运算【例1】(1)设D为△ABC所在平面内一点,𝐵𝐶ሬሬሬሬሬԦ=3𝐶𝐷ሬሬሬሬሬԦ,则()A.AD=-13𝐴𝐵ሬሬሬሬሬԦ+43𝐴𝐶ሬሬሬሬሬԦB.𝐴𝐷ሬሬሬሬሬԦ=13𝐴𝐵ሬሬሬሬሬԦ−43𝐴𝐶ሬሬሬሬሬԦC.𝐴𝐷ሬሬሬሬሬԦ=43𝐴𝐵ሬሬሬሬሬԦ+13𝐴𝐶ሬሬሬሬሬԦD.𝐴𝐷ሬሬሬሬሬԦ=43𝐴𝐵ሬሬሬሬሬԦ−13𝐴𝐶ሬሬሬሬሬԦ(2)设D、E分别是△ABC的边AB、BC上的点,AD=12AB,BE=23BC.若𝐷𝐸ሬሬሬሬሬԦ=λ1𝐴𝐵ሬሬሬሬሬԦ+λ2𝐴𝐶ሬሬሬሬሬԦ(λ1、λ2为实数),则λ1+λ2的值为.知识梳理典例变式基础训练能力提升典例变式【解析】(1) 𝐵𝐶ሬሬሬሬሬԦ=3𝐶𝐷ሬሬሬሬሬԦ,∴𝐶𝐷ሬሬሬሬሬԦ=13𝐵𝐶ሬሬሬሬሬԦ,∴𝐴𝐷ሬሬሬሬሬԦ=𝐴𝐶ሬሬሬሬሬԦ+𝐶𝐷ሬሬሬሬሬԦ=𝐴𝐶ሬሬሬሬሬԦ+13𝐵𝐶ሬሬሬሬሬԦ=𝐴𝐶ሬሬሬሬሬԦ+13(𝐴𝐶ሬሬሬሬሬԦ−𝐴𝐵ሬሬሬሬሬԦ)=-13𝐴𝐵ሬሬሬሬሬԦ+43𝐴𝐶ሬሬሬሬሬԦ.故选A.法二: 𝐵𝐶ሬሬሬሬሬԦ=3𝐶𝐷ሬሬሬሬሬԦ,∴𝐴𝐶ሬሬሬሬሬԦ−𝐴𝐵ሬሬሬሬሬԦ=3(𝐴𝐷ሬሬሬሬሬԦ−𝐴𝐶ሬሬሬሬሬԦ),∴𝐴𝐷ሬሬሬሬሬԦ=-13𝐴𝐵ሬሬሬሬሬԦ+43𝐴𝐶ሬሬሬሬሬԦ.故选A.(2)𝐷𝐸ሬሬሬሬሬԦ=𝐷𝐵ሬሬሬሬሬሬԦ+𝐵𝐸ሬሬሬሬሬԦ=12𝐴𝐵ሬሬሬሬሬԦ+23𝐵𝐶ሬሬሬሬሬԦ=12AB+23(𝐵𝐴ሬሬሬሬሬԦ+𝐴𝐶ሬሬሬሬሬԦ)=-16𝐴𝐵ሬሬሬሬሬԦ+23𝐴𝐶ሬሬሬሬሬԦ,所以λ1=-16,λ2=23,即λ1+λ2=12.【答案】(1)A(2)12知识梳理典例变式基础训练能力提升典例变式【规律方法】平面向量线性运算问题的常见类型及解题策略(1)向量加法或减法的几何意义.向量加法和减法均适合三角形法则.(2)求已知向量的和.一般共起点的向量求和用平行四边形法则;求差用三角形法则;求首尾相连向量的和用三角形法则.(3)求参数问题可以通过研究向量间的关系,通过向量的运算将向量表示出来,进行比较求参数的值.【注意】注意应用初中平面几何的知识如平行线分线段成比例定理、相似三角形的性质等,可以简化运算.知识梳理典例变式基础训练能力提升典例变式变式训练一1.设D为△ABC所在平面内一点,𝐵𝐶ሬሬሬሬሬԦ=3𝐶𝐷ሬሬሬሬሬԦ,则()A.𝐴𝐷ሬሬሬሬሬԦ=-13𝐴𝐵ሬሬሬሬሬԦ+43𝐴𝐶ሬሬሬሬሬԦB.𝐴𝐷ሬሬሬሬሬԦ=13𝐴𝐵ሬሬሬሬሬԦ−43𝐴𝐶ሬሬሬሬሬԦC.𝐴𝐷ሬሬሬሬሬԦ=43𝐴𝐵ሬሬሬሬሬԦ+13𝐴𝐶ሬሬሬሬሬԦD.𝐴...