高考数学总复习 第2讲 一元二次不等式及其解法课件VIP免费

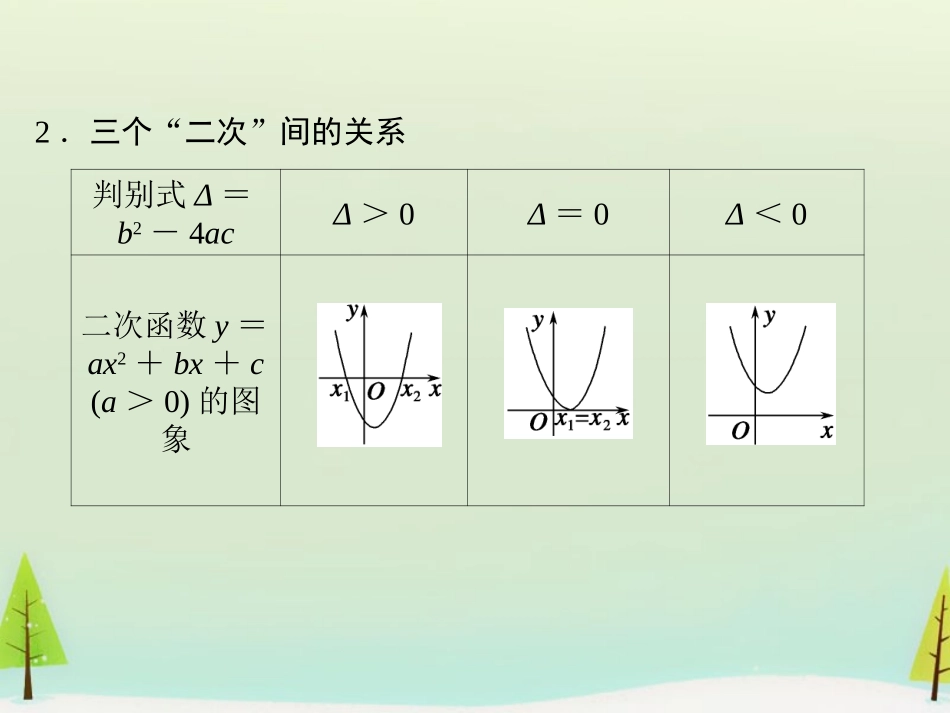
第2讲一元二次不等式及其解法知识梳理1．一元二次不等式的解法(1)将不等式的右边化为零，左边化为二次项系数大于零的不等式ax2＋bx＋c＞0(a＞0)或ax2＋bx＋c＜0(a＞0)．(2)计算相应的判别式．(3)当Δ≥0时，求出相应的一元二次方程的根．(4)利用二次函数的图象与x轴的交点确定一元二次不等式的解集．2．三个“二次”间的关系判别式Δ＝b2－4acΔ＞0Δ＝0Δ＜0二次函数y＝ax2＋bx＋c(a＞0)的图象续表判别式Δ＝b2－4acΔ＞0Δ＝0Δ＜0一元二次方程ax2＋bx＋c＝0(a＞0)的根有两相异实根x1，x2(x1＜x2)有两相等实根没有实数根ax2＋bx＋c＞0(a＞0)的解集Rax2＋bx＋c＜0(a＞0)的解集x1＝x2＝－b2ax|x≠－b2a{x|x＞x2或x＜x1}{x|x1＜x＜x2}∅∅辨析感悟1．对一元二次不等式的解法的理解(1)(教材习题改编)不等式－x2－5x＋6＜0的解集为{x|x＜－6，或x＞1}．(√)(2)若不等式ax2＋bx＋c＜0的解集为(x1，x2)，则必有a＞0.(√)(3)若不等式ax2＋bx＋c＞0的解集是(－∞，x1)∪(x2，＋∞)，则方程ax2＋bx＋c＝0的两个根是x1和x2.(√)(4)若方程ax2＋bx＋c＝0(a≠0)没有实数根，则不等式ax2＋bx＋c＞0的解集为R.(×)2．对一元二次不等式恒成立问题的认识(5)不等式ax2＋bx＋c≤0在R上恒成立的条件是a＜0且Δ＝b2－4ac≤0.(×)(6)若关于x的不等式ax2＋x－1≤0的解集为R，则a≤－14.(√)(7)若不等式x2＋ax＋1≥0对x∈0，12恒成立，则a的最小值为－52.(√)[感悟·提升]三个防范一是当Δ＜0时，不等式ax2＋bx＋c＞0(a≠0)的解集为R还是∅，要注意区别，如(4)中当a＞0时，解集为R；当a＜0时，解集为∅.二是对于不等式ax2＋bx＋c＞0求解时不要忘记讨论a＝0时的情形，如(5)中当a＝b＝0，c≤0时，不等式ax2＋bx＋c≤0在R上也是恒成立的．三是解含参数的一元二次不等式，可先考虑因式分解，再对根的大小进行分类讨论；若不能因式分解，则可对判别式进行分类讨论，分类要不重不漏.考点一一元二次不等式的解法【例1】(2014·大连模拟)已知函数f(x)＝(ax－1)(x＋b)，如果不等式f(x)＞0的解集是(－1,3)，则不等式f(－2x)＜0的解集是________．解析由f(x)＞0，得ax2＋(ab－1)x－b＞0，又其解集是(－1,3)，∴a＜0.且1－aba＝2，－ba＝－3，解得a＝－1或13，∴a＝－1，b＝－3.∴f(x)＝－x2＋2x＋3，∴f(－2x)＝－4x2－4x＋3，由－4x2－4x＋3＜0，得4x2＋4x－3＞0，解得x＞12或x＜－32.答案－∞，－32∪12，＋∞规律方法解一元二次不等式时，当二次项系数为负时要先化为正，再根据判别式符号判断对应方程根的情况，然后结合相应二次函数的图象写出不等式的解集．答案(－∞，－1)【训练1】(2013·江西卷改编)使不等式x<1x0时，原不等式可化为x2＜1＜x3，解得x∈∅，当x＜0时，原不等式可化为x2＞1，x3＜1，解得x＜－1.考点二含参数的一元二次不等式的解法【例2】(2013·烟台期末)解关于x的不等式：ax2－2≥2x－ax(a∈R)．解原不等式可化为ax2＋(a－2)x－2≥0.①当a＝0时，原不等式化为x＋1≤0，解得x≤－1.②当a＞0时，原不等式化为x－2a(x＋1)≥0，解得x≥2a或x≤－1.③当a＜0时，原不等式化为x－2a(x＋1)≤0.当2a＞－1，即a＜－2时，解得－1≤x≤2a；当2a＝－1，即a＝－2时，解得x＝－1满足题意；当2a＜－1，即a＞－2，解得2a≤x≤－1.综上所述，当a＝0时，不等式的解集为{x|x≤－1}；当a＞0时，不等式的解集为xx≥2a，或x≤－1；当－2＜a＜0时，不等式的解集为x2a≤x≤－1；当a＝－2时，不等式的解集为{x|x＝－1}；当a＜－2时，不等式的解集为x－1≤x≤2a.规律方法解含参数的一元二次不等式分类讨论的依据(1)二次项中若含有参数应讨论是小于0，等于0，还是大于0，然后将不等式转化为二次项系数为正的形式．(2)当不等式对应方程的根的个数不确定时，讨论判别式Δ与0的关系．(3)确定无根时可直接写出解集，确定方程有两个根时，要讨论两根的大小关系，从而确定解集形式．【训练2】(1)(2013·...