第五章 三角函数复习课件 新课标 人教版 课件VIP免费

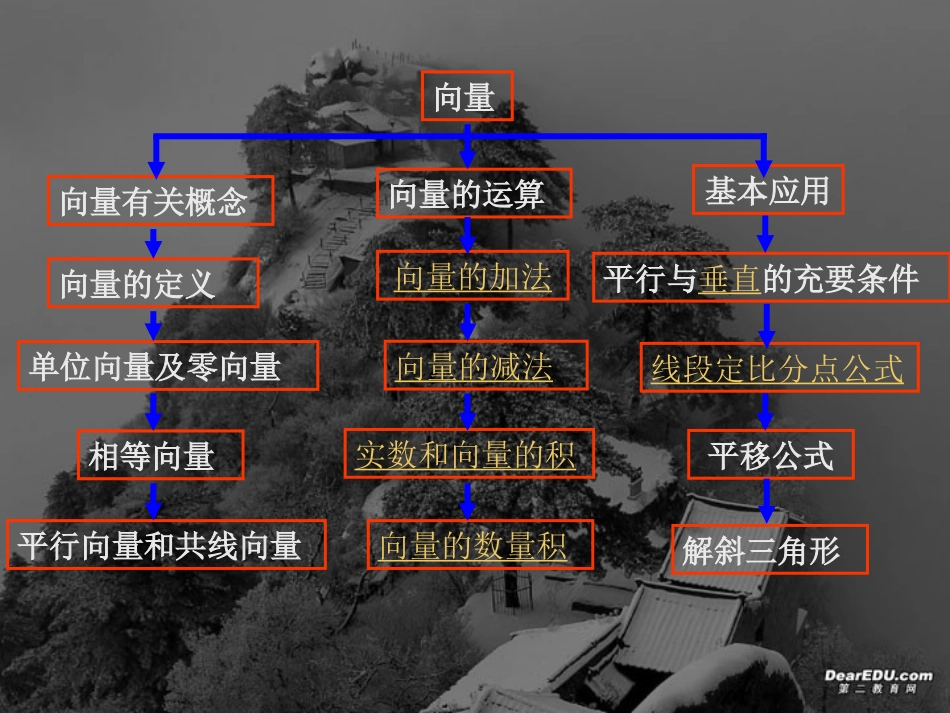
阅读课本小结与复习并讨论阅读课本小结与复习并讨论1.本章内容可分为哪几个部分?2.每一部分有哪些内容?向量向量有关概念向量的运算基本应用向量的定义单位向量及零向量相等向量平行向量和共线向量向量的加法向量的减法实数和向量的积向量的数量积平行与垂直的充要条件线段定比分点公式平移公式解斜三角形向量的加法向量的加法11）加法法则）加法法则2)运算律ab+baab+ba+ba=b+a（交换律））+ba（+c=a++(bc)（结合律）3）坐标运算a=（)X1,Y1b=(,)X2Y2=+ba(,)+X1Y1X2Y2+向量的减法向量的减法11）减法法则）减法法则ab-ab2）坐标运算a=（)X1,Y1b=(,)X2Y2-ab=(-,-)X1Y1X2Y2实数和向量的积1）定义2）运算律3）坐标运算表示：aλa=(x,y)=aλ(λx,λy)λ(μ)=(λμ)aa+μa(λ+μ)a=aλa+baλ()=λ+μa向量的数量积1)1)定义定义ab.=abcosθ2)运算律ab.=b.a）aλ（.b=b（λa.）=λ（ab.）=.c（+ba）.ba.c+.c3）坐标运算a=（)X1,Y1b=(,)X2Y2ab.=+X1Y2X2Y1平行与垂直的充要条件a‖ba=λbX1Y1X2Y2-=0=0aab.+X1Y2X2Y1=0⊥b1）平行充要条件2）垂直的充要条件线段定比分点公式线段定比分点公式设设P(x,y),PP(x,y),P11(x(x11,y,y11),P),P22(x(x22,y,y22))且且PP分有向分有向线段线段PP11PP22所成比为所成比为λ，则有中点坐标公式:X=1+λX1+λx2y=1+λY1+λY2X=2X1+x2y=2Y1+Y2平移公式平移公式如果点如果点P(x,y)P(x,y)按向量按向量aa(h,k)(h,k)平移至平移至P’(x’,y’)P’(x’,y’)，则有，则有X’=x+hY’=y+k正正..余弦定理余弦定理正弦定理正弦定理余弦定理余弦定理asinA=bsinBcsinC==2Ra2b2=+c2-2bccosAa2b2c2=+-2cacosBa2b2c2=+-2abcosC（5）a·b的性质。①e·a=a·e=|a|cosθ②a⊥ba·b=0③a，b同向a·b=|a||b|反向时a·b=-|a|·|b|a2=a·a=|a|2(a·a=)④cosθ=⑤|a·b|≤|a|·|b|（6）a·b运算律①a·b=b·a②(λa)·b=λ(a·b)=a·(λb)③(a+b)c=a·c+b·c（7）平面向量数量积的坐标表示。①若a=(x1,y1)b=(x2,y2)则a.b=x1x2+y1y2②若a=(x,y)则|a|2=x2+y2|a|=③A(x1,y1)B(x2,y2)|AB|=④若a=(x1,y1)b=(x2,y2)则a⊥bx1x2+y1y2=0平面向量复习知识结构巩固练习巩固练习课外作业课外作业知识要点例题解析例1化简（1）（AB+MB）+BO+OM（2）AB+DA+BD－BC－CA分析利用加法减法运算法则，借助结论AB=AP+PB；AB=OB－OA；AB+BC+CA=0进行变形.解：原式=AB+（BO+OM+MB）=AB+0=AB（1）（2）原式=AB+BD+DA－（BC+CA）=0－BA=AB例1平面向量复习知识结构巩固练习巩固练习课外作业课外作业知识要点例题解析例2设AB=2(a+5b)，BC=2a+8b，CD=3(ab)，求证：A、B、D三点共线。分析要证A、B、D三点共线，可证AB=λBD关键是找到λ解： BD=BC+CD=2a+8b+3(ab)=a+5b∴AB=2BD且AB与BD有公共点B∴A、B、D三点共线AB∥BD例3例3已知a=(3,-2)b=(-2,1)c=(7,-4)，用a、b表示c。解：设c=ma+nb(7,-4)=m(3,-2)+n(-2,1)3m-2n=7m=1-2m+n=-4n=-2c=a-2b解:9=9a2+4b2-12a·b∴a·b=(3a+b)2=9a2+b2+6a·b=12∴|3a+b|=2例5a=(3,-5)b=(-4,-2),则a·b=向量a在向量b的投影为——解：a·b=x1x2+y1y2=-12+10=-2例4设|a|=|b|=1|3a-2b|=3则|3a+b|=____分析,关键求|a|,|b|,a·b例6|a|=10b=(3,-4)且a∥b求a|a|=10b=(3,-4)且a⊥b求a解：设a=(x,y)则-4x=3yx=6x=-6y=-8y=8a=(6,-8)或(-6,8)例7已知A（1，-3），B（0，2），C（-1，1）,点D在直线BC上,若设D(x,y),则解：例8、（1）已知a,b都是非零向量，且a+3b与7a-5b垂直,a-4b与7a-2b垂直，求a与b的夹角；(2)已知|a|=,|b|=，且a与b的夹角为，试求a+2b与a-b的夹角Q的大小。解：（1）(a+3b)·(7a-5b)=0(a-4b)·(7a-2b)=07a2+16a·b-15b2=07a2-30a·b+8b2=0a2=b22a·b=b2∴cosθ=∴θ=60。（2）a2=3b2=4|a|·|b|=2a·b=|a|·|b|cosθ=·cos30。=3(2)已知|a|=,|b|=，且a与b的夹角为，试求a+2b与a-b的夹角Q的大小。6、平移（1）定义。（2）公式:P(x,y)为F上任一点。P′(x′,y′)为平移后P对应点.PP′=(h,k)x′=x+hy′=y+k例11A(-3,4),B(1,3)按a=(2,-4)平移，平移后对应点A′,B′坐标。x′=-3+2=-1y′=4-4=0A′(-1,0),B′(3,-1)例12y=x2图象按a平移后得图象与y=2x-5图象只有一个公共点(3,1)求a解...