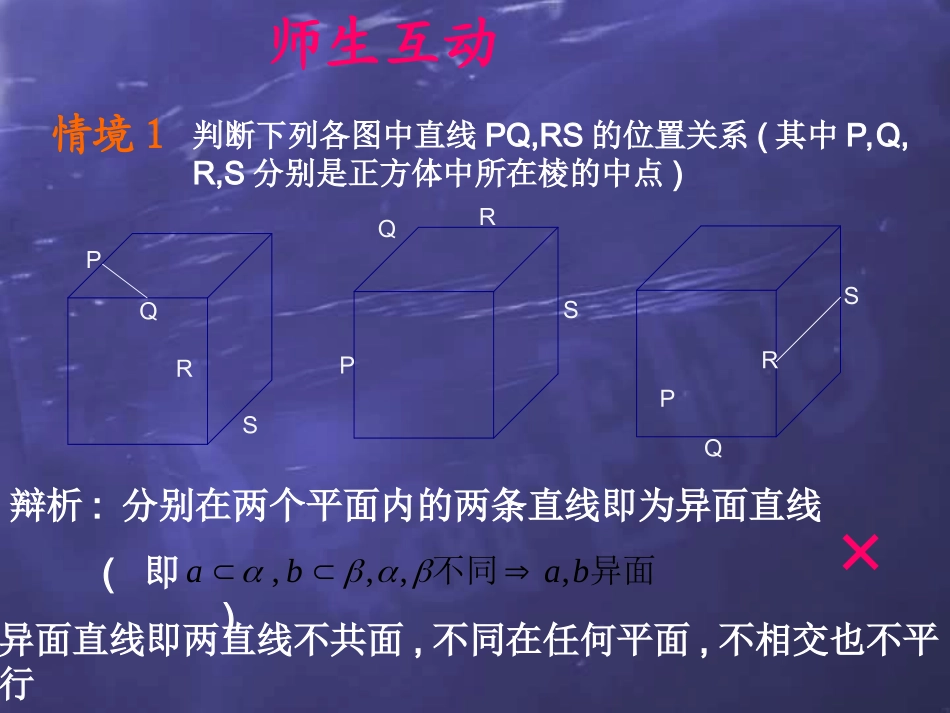
海安县李堡中学高一数学组空间两条直线的位置关系(二)异面直线情境1判断下列各图中直线PQ,RS的位置关系(其中P,Q,R,S分别是正方体中所在棱的中点)SRQPSRQPSRQP师生互动辩析:分别在两个平面内的两条直线即为异面直线(即)异面不同baba,,,,×异面直线即两直线不共面,不同在任何平面,不相交也不平行情境2与A1C具有怎样的位置关系?在正方体ABCD-A1B1C1D1中,直线AB异面DCBAA1D1C1B1为何(异面)不共面?情境3师生互动DCBAA1D1C1B1假设AB与A1C共面,过点C和AB的平面只有一个.所以直线A1C和AB都应在ABCD内.于是点A1在平面ABCD内.这与点A1在平面ABCD外矛盾,所以直线A1C和AB是异面直线.αBA结论:过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线αBAlαBαAαBlAB与l异面情境3:平面几何中a与b是相交直线,a与c也是相交直线,它们之间可以用什么来区别?情境4:直线a与b,直线a与c,都是异面直线.b,c的位置关系如何?我们该如何区别?acbM师生互动定义:异面直线所成的角a,b是两条异面直线,经过空间任意一点o,分别引直线a1∥a,b1∥b,我们把直线a1和b1所成的锐角(或直角)叫做异面直线a和b所成的角aα若两条异面直线a,b所成角是直角,则称这两条异面直线互相垂直,记a⊥b(空间垂直包括相交垂直,异面垂直)范围:0°<θ≤90°角的大小与点o的位置无关bOa1b1说明:构建数学BCDEFA1.作出空间四边形ABCD中异面直线AE,CF所成的角数学运用2.a,b是两条异面直线,A,B是a上的两点,C,D是b上的两点,且AB=8,CD=6,P,Q,R分别是AC,BD,AD的中点(1)证明:∠PRQ为异面直线a,b所成的角或补角(2)若PQ=5,证明:a⊥bABDCPbaQR数学运用已知ABCD-A1B1C1D1是棱长为a的正方体例3.(1)正方体的哪些棱所在的直线与直线BC1是异面直线?(2)求异面直线AA1与BC所成的角.(3)求异面直线BC1和AC所成的角.①平移②特殊点DCBAA1D1C1B1解.(1)与BC1是异面直线的是A1A,A1B1,A1D1,DA,DC,DD1(2)∵BB1∥AA1,∴∠B1BC为AA1与BC所成角∵∠B1BC=90°∴AA1与BC所成角为90°DCBAA1D1C1B1∴四边形AA1C1C是∴AC∥A1C1∵∠BC1A1为BC1与A1C1所成的角∵A1B=BC1=A1C1所以,异面直线BC1和AC所成角为60°(3)因为AA1BB1CC1∥∥∴∠BC1A1=60°《《异面直线》教学过程异面直线》教学过程空间两条直线的位置关系①本节学习了重要概念:两异面直线所成的角②两异面直线所成的角满足0°<θ≤90°通常采用平移的方法化异面直线为相交直线所成的角P29:第8,第9,第11,第12---(3)