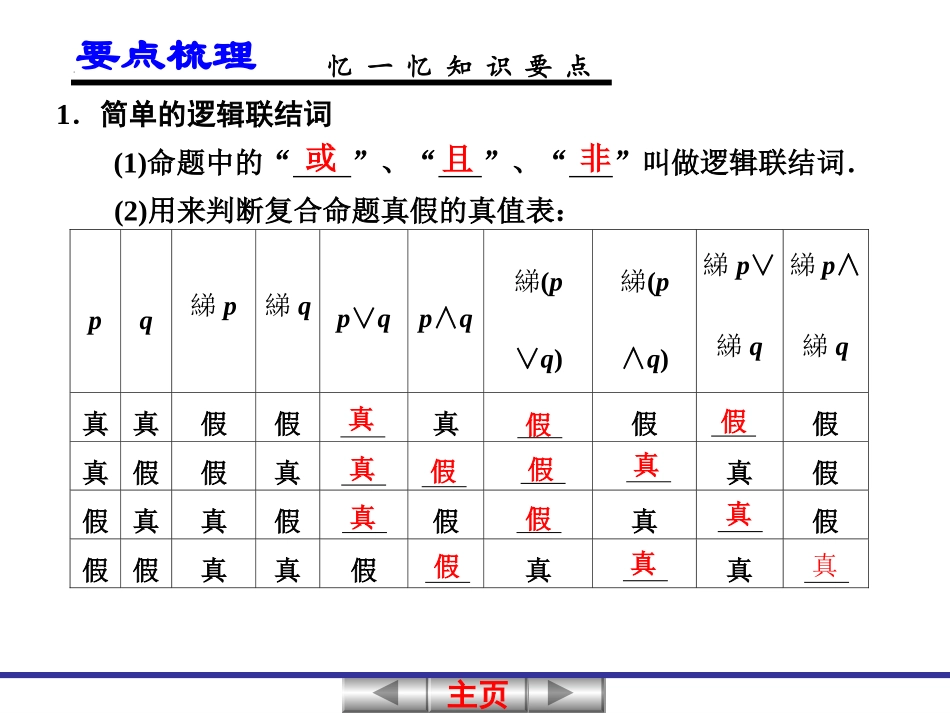
主页主页主页主页一轮复习讲义一轮复习讲义简单的逻辑联结词、全称量词与存在量词主页主页主页主页1.简单的逻辑联结词(1)命题中的“”、“”、“”叫做逻辑联结词.(2)用来判断复合命题真假的真值表:pq綈p綈qp∨qp∧q綈(p∨q)綈(p∧q)綈p∨綈q綈p∧綈q真真假假真假假真假假真真假假真真假假真假假假真真假真真要点梳理忆一忆知识要点或且非真真真假假假假假真真真真假主页主页主页主页2.全称量词与存在量词(1)常见的全称量词有:“任意一个”、“一切”、“每一个”、“所有的”等.(2)常见的存在量词有:“存在一个”、“至少有一个”、“有些”、“有一个”、“某个”、“有的”等.(3)全称量词用符号“”表示;存在量词用符号“”表示.(4)全称命题与存在性命题①的命题叫全称命题.②的命题叫存在性命题.忆一忆知识要点∀∃含有全称量词含有存在量词要点梳理主页主页主页主页3.命题的否定(1)全称命题的否定是存在性命题;存在性命题的否定是全称命题.(2)“p或q”的否定为:“非p且非q”;“p且q”的否定为:“非p或非q”.忆一忆知识要点要点梳理主页主页主页主页[难点正本疑点清源]1.逻辑联结词“或”的含义有三种逻辑联结词中的“或”的含义,与并集概念中的“或”的含义相同.如“x∈A或x∈B”,是指:x∈A且x∉B;x∉A且x∈B;x∈A且x∈B三种情况.再如“p真或q真”是指:p真且q假;p假且q真;p真且q真三种情况.因此,在遇到逻辑联结词“或”时,要注意分析三种情况.主页主页主页主页2.正确区别:命题的否定与否命题“否命题”是对原命题“若p,则q”的条件和结论分别加以否定而得到的命题,它既否定其条件,又否定其结论;“命题的否定”即“非p”,只是否定命题p的结论.命题的否定与原命题的真假总是对立的,即两者中有且只有一个为真,而原命题与否命题的真假无必然联系.主页主页主页主页例1已知命题p1:函数y=2x-2-x在R上为增函数,p2:函数y=2x+2-x在R上为减函数,则在命题q1:p1∨p2,q2:p1∧p2,q3:(綈p1)∨p2和q4:p1∧(綈p2)中,真命题是________.含有逻辑联结词命题的真假含有逻辑联结词命题的真假判断判断先判断p1和p2的真假,然后对用逻辑联结词构成的复合命题进行真假判断.主页主页主页主页因为y=2x为增函数,y=2-x为减函数,所以p1:y=2x-2-x在R上为增函数为真命题,p2:y=2x+2-x在R上为减函数为假命题.即綈p2为真命题.所以q1,q4为真命题.答案q1,q4解析解析主页主页主页主页(1)判断含有逻辑联结词的复合命题的真假,关键是对逻辑联结词“且”“或”“非”含义的理解.(2)解决该类问题的基本步骤:①弄清构成复合命题中简单命题p和q的真假;②明确其构成形式;③根据复合命题真假规律判断构成新命题的真假.探究提高主页主页主页主页写出由下列各组命题构成的“p∨q”、“p∧q”、“綈p”形式的复合命题,并判断真假.(1)p:1是素数;q:1是方程x2+2x-3=0的根;(2)p:平行四边形的对角线相等;q:平行四边形的对角线互相垂直;(3)p:方程x2+x-1=0的两实根的符号相同;q:方程x2+x-1=0的两实根的绝对值相等.变式训练1(1)p∨q:1是素数或是方程x2+2x-3=0的根.真命题.p∧q:1既是素数又是方程x2+2x-3=0的根.假命题.綈p:1不是素数.真命题.解析解析主页主页主页主页(2)p∨q:平行四边形的对角线相等或互相垂直.假命题.p∧q:平行四边形的对角相等且互相垂直.假命题.綈p:有些平行四边形的对角线不相等.真命题.(3)p∨q:方程x2+x-1=0的两实根的符号相同或绝对值相等.假命题.p∧q:方程x2+x-1=0的两实根的符号相同且绝对值相等.假命题.綈p:方程x2+x-1=0的两实根的符号不相同.真命题.主页主页主页主页例2写出下列命题的否定,并判断其真假.(1)p:∀x∈R,x2-x+14≥0;(2)q:所有的正方形都是矩形;(3)r:∃x0∈R,x20+2x0+2≤0;(4)s:至少有一个实数x0,使x30+1=0.含有一个量词的命题的否定否定量词,否定结论,写出命题的否定;判断命题的真假.主页主页主页主页(1)綈p:∃x0∈R,x20-x0+14<0,假命题.(2)綈q:至少存在一个正方形不是矩形,假命题.(3)綈r:∀x∈R,x2...