高考数学一轮总复习名师精讲 第48讲空间向量的坐标运算课件VIP免费

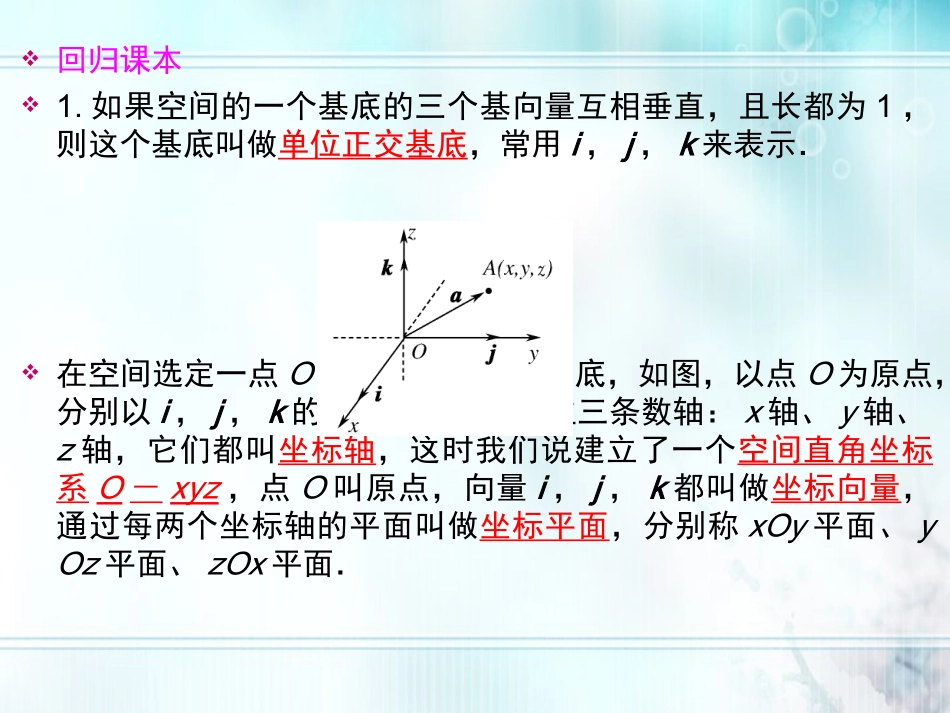
第四十八讲(第四十九讲(文))空间向量的坐标运算回归课本1.如果空间的一个基底的三个基向量互相垂直，且长都为1，则这个基底叫做单位正交基底，常用i，j，k来表示．在空间选定一点O和一个单位正交基底，如图，以点O为原点，分别以i，j，k的方向为正方向建立三条数轴：x轴、y轴、z轴，它们都叫坐标轴，这时我们说建立了一个空间直角坐标系O－xyz，点O叫原点，向量i，j，k都叫做坐标向量，通过每两个坐标轴的平面叫做坐标平面，分别称xOy平面、yOz平面、zOx平面．作空间直角坐标系O－xyz时，一般使∠xOy＝135°，∠yOz＝90°.对于空间任一向量a，由空间向量的基本定理，存在唯一的有序实数组(a1，a2，a3)，使a＝a1i＋a2j＋a3k.有序实数组(a1，a2，a3)叫做a在空间直角坐标系O－xyz中的坐标，记为a＝(a1，a2，a3)．对于空间任一点A，对应一个向量，于是存在唯一的有序实数组x，y，z，使＝xi＋yj＋zk，即点A的坐标为(x，y，z)．2．向量的直角坐标运算设a＝(a1，a2，a3)，b＝(b1，b2，b3)，则a＋b＝(a1＋b1，a2＋b2，a3＋b3)；a－b＝(a1－b1，a2－b2，a3－b3)；a·b＝a1b1＋a2b2＋a3b3；a∥b⇔a＝λb⇔a1＝λb1，a2＝λb2，a3＝λb3(λ∈R)或＝＝(b1，b2，b3均不为0)．a⊥b⇔a·b＝0⇔a1b1＋a2b2＋a3b3＝0.设A(x1，y1，z1)，B(x2，y2，z2)，则＝－＝(x2，y2，z2)－(x1，y1，z1)＝(x2－x1，y2－y1，z2－z1)；这就是说，一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去始点的坐标．3．夹角和距离公式设a＝(a1，a2，a3)，b＝(b1，b2，b3)，则|a|＝a·a＝a12＋a22＋a32|b|＝b·b＝b12＋b22＋b32cos〈a，b〉＝a·b|a|·|b|＝a1b1＋a2b2＋a3b3a12＋a22＋a32b12＋b22＋b32.在空间直角坐标系(图)中，已知A(x1，y1，z1)，B(x2，y2，z2)，则dA，B＝|AB→|＝AB→·AB→＝x2－x12＋y2－y12＋z2－z12.其中dA，B表示A与B两点间的距离，这就是空间两点间的距离公式．答案：C考点陪练1.(2011·武汉)已知A(1,0,0)，B(0，－1,1)，OA→＋λOB→与OB→的夹角为120°，则λ的值为()A．±66B.66C．－66D．±6答案：B2．已知a＝1，－32，52，b＝－3，λ，－152，且a∥b，则λ等于()A.23B.92C．－92D．－23解析：由1－3＝－32λ＝52－152，可知λ＝92.答案：B3．已知a·b＝0且a＝(2，－3,5)，则b可以是()A.12，－13，15B.12，13，0C.－12，13，15D．(0,3,3)解析：采用代入验证法知12×2－3×13＋5×0＝0.答案：D4．已知a＝(1,1,0)，b＝(－1,0,2)，且ka＋b与2a－b互相垂直，则k的值是()A．1B.15C.35D.75解析：|a|＝2，|b|＝5，a·b＝－1＋0＋0＝－1，(ka＋b)⊥(2a－b)⇒(ka＋b)·(2a－b)＝0⇒2k|a|2－|b|2＋(2－k)a·b＝0⇒2k×2－5＋(2－k)·(－1)＝0⇒k＝75.答案：A5．已知a＝(2，－1,2)，b＝(2,2,1)，则以a，b为邻边的平行四边形的面积为()A.65B.652C．4D．8解析：由a·b＝2×2＋(－1)×2＋2×1＝4，|a|＝3，|b|＝3，cos〈a，b〉＝49.∴sin〈a，b〉＝659，∴S＝|a|·|b|·sin〈a，b〉＝65.应选A.类型一空间向量的坐标运算解题准备：向量坐标的运算，就是向量的同名坐标之间的代数运算，向量相等就是对应坐标相等．要注意区分点的坐标与向量的坐标的关系．【典例1】设向量a＝(3,5，－4)，b＝(2,1,8)，计算2a＋3b,3a－2b，a·b以及a与b所成的角的余弦值，并确定λ，μ的值，使λa＋μb与z轴垂直．[分析]要计算2a＋3b,3a－2b及a·b，只要代入向量坐标运算的公式即可．求a与b所成的角的余弦值，应先求出|a|及|b|，代入公式cos〈a，b〉＝a·b|a|·|b|即可．而要使λa＋μb与z轴垂直，只要使(λa＋μb)·(0,0,1)＝0，从而转化为λ，μ的方程组进而求出λ，μ的值．[解析]2a＋3b＝2(3,5，－4)＋3(2,1,8)＝(12,13,16)，3a－2b＝3(3,5，－4)－2(2,1,8)＝(5,13，－28)，a·b＝(3,5，－4)·(2,1,8)＝3×2＋5×1－4×8＝－21，|a|＝32＋52＋－42＝50，|b|＝22＋12＋82＝69，∴cos〈a，b〉＝a·b|a||b|＝－2150·69＝－7138230，由(λa＋μb)·(0,0,1)＝(3λ＋...