高三数学一轮复习 第五章 第2课时 等差数列及其前n项和课件 文 新人教A版 课件VIP免费

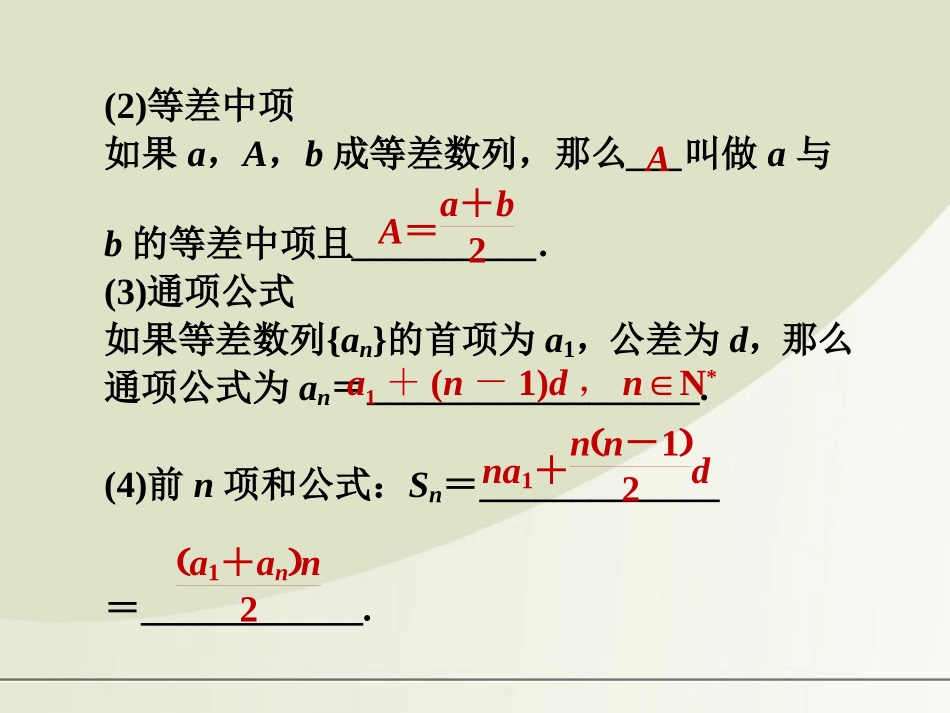
第2课时等差数列及其前n项和1．等差数列的有关概念(1)等差数列的定义如果一个数列从第__项起，每一项与它的前一项的差等于____________，那么这个数列就叫做等差数列，这个常数叫做等差数列的_____，通常用字母__表示，定义的表达式为___________.同一个常数2公差an＋1－an＝dd(2)等差中项如果a，A，b成等差数列，那么___叫做a与b的等差中项且__________.(3)通项公式如果等差数列{an}的首项为a1，公差为d，那么通项公式为an＝__________________.(4)前n项和公式：Sn＝_____________＝____________.AA＝a＋b2a1＋(n－1)d，n∈N*na1＋nn－12da1＋ann2【思考探究】A＝a＋b2是a，A，b成等差数列的什么条件？提示：充要条件．若A＝a＋b2⇒2A＝a＋b⇒A－a＝b－A⇒a，A，b成等差数列．反之，若a，A，b成等差数列，则A＝a＋b2.故A＝a＋b2是a，A，b成等差数列的充要条件．2．等差数列的性质已知数列{an}是等差数列，Sn是其前n项和．(1)若m＋n＝p＋q，则______________.特别：若m＋n＝2p，则am＋an＝2ap.(2)am，am＋k，am＋2k，am＋3k，…仍是等差数列，公差为_____.(3)数列Sm，S2m－Sm，S3m－S2m，…也是等差数列．am＋an＝ap＋aqkd1．(2010·重庆卷)在等差数列{an}中，a1＋a9＝10，则a5的值为()A．5B．6C．8D．10解析：在等差数列{an}中，2a5＝a1＋a9＝10，∴a5＝5.答案：A2．{an}为等差数列，且a7－2a4＝－1，a3＝0，则公差d＝()A．－2B．－12C.12D．2解析：根据题意得a7－2a4＝a1＋6d－2(a1＋3d)＝－1，∴a1＝1.又 a3＝a1＋2d＝0，∴d＝－12.答案：B3．等差数列{an}的公差d＜0，且a2·a4＝12，a2＋a4＝8，则数列{an}的通项公式是()A．an＝2n－2(n∈N*)B．an＝2n＋4(n∈N*)C．an＝－2n＋12(n∈N*)D．an＝－2n＋10(n∈N*)解析：由a2·a4＝12，a2＋a4＝8，d＜0，⇒a2＝6，a4＝2.⇒a1＝8，d＝－2，所以an＝a1＋(n－1)d，即an＝8＋(n－1)(－2)得an＝－2n＋10，故选D.答案：D4．设等差数列{an}的前n项和为Sn，若a6＝S3＝12，则{an}的通项an＝________.解析：设等差数列首项为a1，公差为d，则a1＋5d＝12，3a1＋3×22d＝12，即a1＋5d＝12，a1＋d＝4，∴a1＝2，d＝2.an＝a1＋(n－1)d＝2n.答案：2n5．数列{an}中，a1＝15,3an＋1＝3an－2(n∈N*)，则该数列中乘积是负值的相邻两项为________．解析：由已知得an＋1－an＝－23，a1＝15，∴an＝a1＋(n－1)d＝15－23(n－1)＝47－2n3，显然a23＞0，a24＜0.∴该数列中乘积是负值的相邻两项为a23与a24.答案：第23项与第24项等差数列的判断与证明判断或证明数列{an}为等差数列，常见的方法有以下几种：(1)利用定义：an＋1－an＝d(常数)(n∈N*)；(2)利用等差中项：2an＋1＝an＋an＋2；(3)利用通项公式：an＝dn＋c(d、c为常数)，d为公差．当d≠0时，通项公式an是关于n的一次函数；d＝0时为常函数，也是等差数列；(4)利用前n项和公式：Sn＝an2＋bn(a、b为常数)．若一个数列的前n项和为关于n的二次函数且不含常数项，则这个数列为公差不等于零的等差数列；若此时的a＝0，则此数列为常数列．已知数列{an}中，a1＝35，an＝2－1an－1(n≥2，n∈N*)，数列{bn}满足bn＝1an－1(n∈N*)．(1)求证：数列{bn}是等差数列；(2)求数列{an}中的最大项和最小项，并说明理由．解析：(1)证明： an＝2－1an－1(n≥2，n∈N*)，bn＝1an－1.∴n≥2时，bn－bn－1＝1an－1－1an－1－1＝12－1an－1－1－1an－1－1＝an－1an－1－1－1an－1－1＝1.又b1＝1a1－1＝－52.∴数列{bn}是以－52为首项，以1为公差的等差数列．(2)由(1)知，bn＝n－72，则an＝1＋1bn＝1＋22n－7，设函数f(x)＝1＋22x－7，易知f(x)在区间－∞，72和72，＋∞内为减函数，∴当n＝3时，an取得最小值－1；当n＝4时，an取得最大值3.【变式训练】1.(2011·浙江台州一模)数列{an}中，a1＝1，当n≥2时，其前n项的和Sn满足S2n＝an(Sn－1)．证明：数列1Sn是等差数列．证明： S2n＝an(Sn－1)，∴S2n＝(Sn－Sn－1)(Sn－1)(n≥2)．∴SnSn－1＝Sn－1－Sn，即1Sn－1Sn－1＝1.∴1Sn...