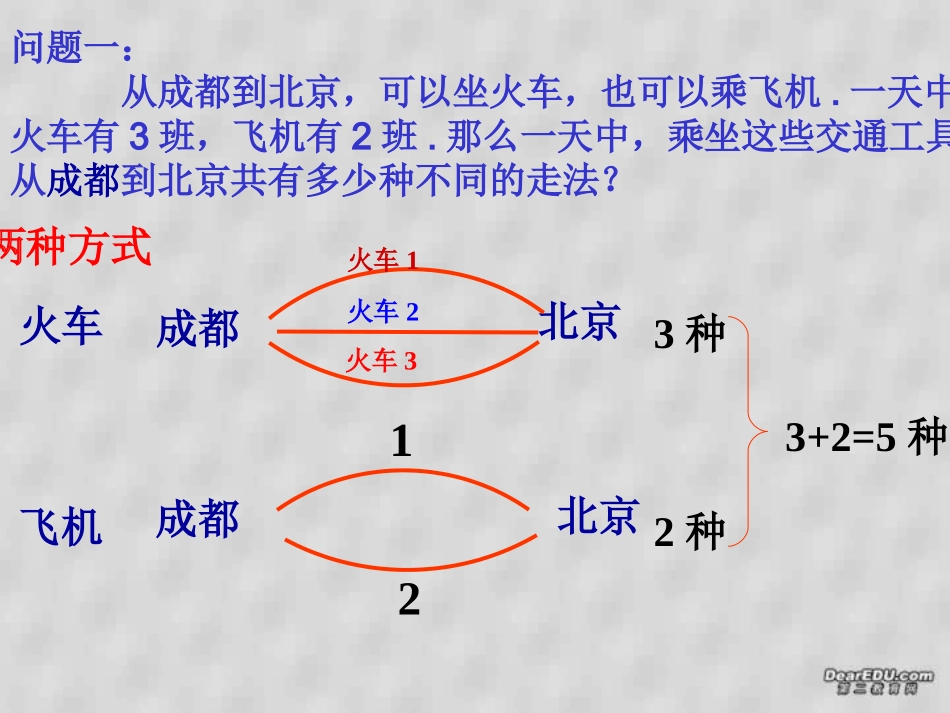
分类计数原分类计数原理与分步计理与分步计数原理数原理成都北京成都北京13种2种23+2=5种问题一:从成都到北京,可以坐火车,也可以乘飞机.一天中,火车有3班,飞机有2班.那么一天中,乘坐这些交通工具从成都到北京共有多少种不同的走法?火车2两种方式火车飞机火车1火车3现有高中一年级的学生3名,高中二年级的学生5名,高中三年级的学生4名.从中任选1人参加接待外宾的活动,有多少种不同的选法?N=3+5+4=12引例引例22一、分类计数原理一、分类计数原理完成一件事,有n类办法.在第1类办法中有m1种不同的方法,在第2类方法中有m2种不同的方法,……,在第n类方法中有mn种不同的方法,则完成这件事共有2)首先要根据具体的问题确定一个分类标准,在分类标准下进行分类,然后对每类方法计数.1)各类办法之间相互独立,都能独立的完成这件事,要计算方法种数,只需将各类方法数相加,因此分类计数原理又称加法原理说明说明N=m1+m2+…+mn种不同的方法先乘汽车再乘火车泸州成都123北京12汽车1火车1火车2汽车2火车1火车2汽车3火车2火车13×2=6种引例引例33现有高中一年级的学生3名,高中二年级的学生5名,高中三年级的学生4名,从3个年级的学生中各选1人参加接待外宾的活动,有多少种不同的选法?N=3×5×4=60引例引例44二、分步计数原理二、分步计数原理完成一件事,需要分成n个步骤。做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,则完成这件事共有2)首先要根据具体问题的特点确定一个分步的标准,然后对每步方法计数.1)各个步骤相互依存,只有各个步骤都完成了,这件事才算完成,将各个步骤的方法数相乘得到完成这件事的方法总数,又称乘法原理说明说明N=m1×m2×…×mn种不同的方法加法原理乘法原理联系区别一完成一件事情共有n类办法,关键词是“分类”完成一件事情,共分n个步骤,关键词是“分步”区别二每类办法都能独立完成这件事情。每一步得到的只是中间结果,任何一步都不能能独立完成这件事情,缺少任何一步也不能完成这件事情,只有每个步骤完成了,才能完成这件事情。分类计数原理和分步计数原理,回答的都是关于完成一件事情的不同方法的种数的问题。区别三各类办法是互斥的、并列的、独立的各步之间是相关联的分类计数与分步计数原理的区别和联系:例1图书馆的书架上第1层放有4本不同的《读者》,第2层放有3本不同的《小小说月刊》,第3层放有2本不同的体育杂志(2)从书架的第1、2、3层各取1本书,有多少种不同取法?(1)、N=4+3+2=9(2)、N=4×3×2=24(1)从书架上任取1本书,有多少种不同的取法?例2、一种号码锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成多少个四位数字号码。10*10*10*10=10000例3、要从甲乙丙3人中选出2人分别上日班和晚班,有多少种不同的选法。3*2=6例3、在红色信箱中有30封观众来信,在蓝色信箱中有20封观众来信,若先确定一名幸运之星,然后再从两信箱中各确定一名幸运伙伴,会产生多少种不同的结果?30封20封302920××=17400共28800种201930××=114002、把5封信投入6个邮箱,不同的投法共有()A、65种B、56种C、720种D、30种1、3名同学报名参加4个不同学科的比赛,每名学生只能参赛一项,有多少种不同的报名方案?N=4×4×4=64A思考练习题思考练习题3、集合A={a,b,c}B={1,2}。则集合A到集合B的映射有多少个?集合B到集合A的映射有多少个?集合A到集合B的映射有2*2*2=23个{a,b,c}{1,2}{a,b,c}{1,2}{a,b,c}{1,2}{a,b,c}{1,2}{a,b,c}{1,2}{a,b,c}{1,2}{a,b,c}{1,2}{a,b,c}{1,2}由映射的定义,元素a只能由1或2中的一个与之对应有2种方法,b、c同理,分布完成,所以为233、如图,小圆圈表示网络的结点,结点之间的连线表示它们之间有网线相连,连线标注的数字表示该网线单位时间内可通过的最大信息量,现从A点向B点传递信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为()A、26B、24C、20D、19D。。。。。。MN54。F67ED86CB。A121263沿A-C-D-B,沿A-C-M-B,沿A-E-N-B,沿A-E-F-B,传递的最大信息量为3分析:传递的最大信息量为4传递的最大信息量为6传递的最大信息量为6由分类计数原理可得最大信息量为N=3+4+6+6=19从A到B有四条路线作业:完成资料上的题谢谢:祝同学们学习进步,身心健康。