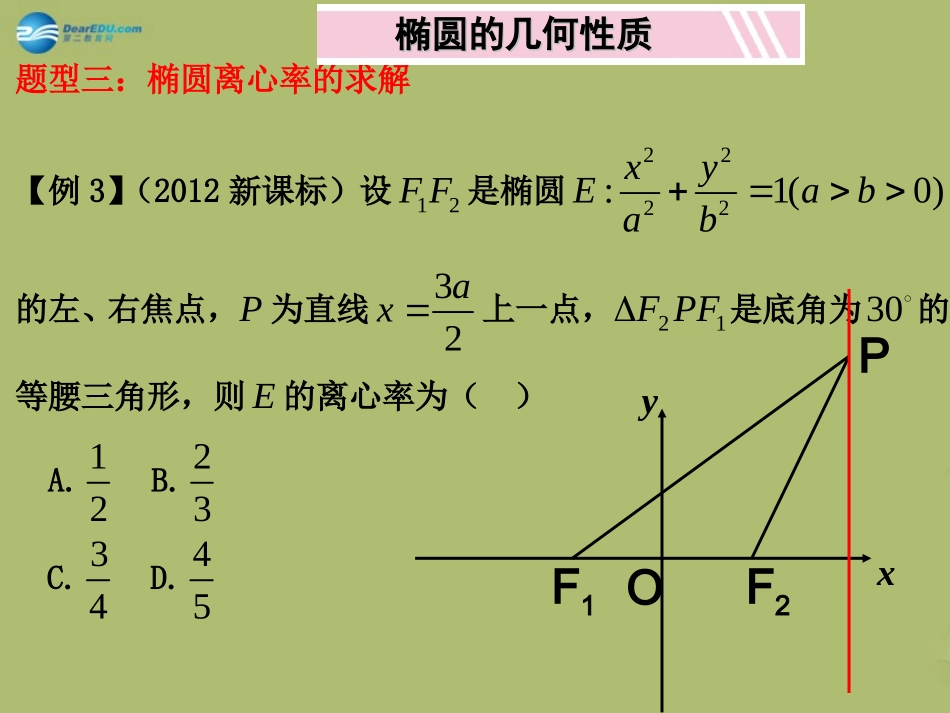
直线与椭圆的位置关系4.椭圆的对称轴在坐标轴上,长轴是短轴的2倍,且过点(2,1),则它的方程是__________.典型错例(课后巩固):注意椭圆的基本量的变化!题型三:椭圆离心率的求解【例3】(2012新课标)设12FF是椭圆2222:1(0)xyEabab的左、右焦点,P为直线32ax上一点,12PFF是底角为30的等腰三角形,则E的离心率为()A.12B.23C.D.椭圆的几何性质椭圆的几何性质F1F2POyx(1)椭圆上一点与两焦点构成的三角形,称为椭圆的焦点三角形,与焦点三角形有关的计算或证明常利用正弦定理、余弦定理、122PFPFa+=,得到a、c的关系.(2)对△F1PF2的处理方法定义式的平方余弦定理面积公式⇔(PF1+PF2)2=(2a)24c2=PF21+PF22-2PF1·PF2cosθS△=12PF1·PF2sinθ.探究提高题型三:椭圆离心率的求解(2)已知关于x的一元二次方程220axbxc有两个不同的实根,则椭圆22221(0)xyabab的离心率的取值范围是()A.51(0,)2B.51(,1)2C.52(,1)2例3.已知P是椭圆上一点,12,FF分别是椭圆的左右焦点,且12PFPF,求离心率的取值范围.解:当点P在椭圆短轴端点时,12FPF最大.45≥2sin2≥2sin2ca≥xF1F2oyP01e又≤212e题型四:直线与椭圆的位置关系[2012北京)已知椭圆C:22221(0)xyabab的一个顶点为(2,0)A,离心率为22.直线(1ykx)与椭圆C交于不同的两点M,N.(Ⅰ)求椭圆C的方程;(Ⅱ)当△AMN得面积为103时,求k的值.“方程思想!”(1)解答直线与椭圆的题目时,时常把两个曲线的方程联立,消去x(或y)建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系.(2)涉及到直线方程的设法时,务必考虑全面,求解中,常因忽略直线l的特殊形式而失分.探究提高[2014·新课标全国卷Ⅰ]已知点A(0,-2),椭圆E:x2a2+y2b2=1(a>b>0)的离心率为32,F是椭圆E的右焦点,直线AF的斜率为233,O为坐标原点.(1)求E的方程;(2)设过点A的动直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.解:(1)设F(c,0),由条件知,2c=233,得c=3.又ca=32,所以a=2,b2=a2-c2=1.故E的方程为x24+y2=1.(2)当l⊥x轴时不合题意,故可设l:y=kx-2,P(x1,y1),Q(x2,y2).将y=kx-2代入x24+y2=1得(1+4k2)x2-16kx+12=0,当Δ=16(4k2-3)>0,即k2>34时,x1,2=8k±24k2-34k2+1,从而|PQ|=k2+1|x1-x2|=4k2+1·4k2-34k2+1.又点O到直线l的距离d=2k2+1.所以△OPQ的面积S△OPQ=12d·|PQ|=44k2-34k2+1.设4k2-3=t,则t>0,S△OPQ=4tt2+4=4t+4t.因为t+4t≥4,当且仅当t=2,即k=±72时等号成立,满足Δ>0,所以,当△OPQ的面积最大时,k=±72,l的方程为y=72x-2或y=-72x-2.例1.(07陕西)此时3313.224S22221||(1)()ABkxx2(1)k3312.222S跟踪训练:(本小题满分12分)已知定圆22:(3)16Mxy,动圆N过点(3,0)F且与圆M相切,记圆心N的轨迹为E(1)求轨迹E的方程;(2)设点,,ABC在E上运动,A与B关于原点对称,且ACCB,当ABC的面积最小时,求直线AB的方程。【解析】(1)(2)y=x或y=﹣x解析:解:(Ⅰ)因为点在圆内,所以圆N内切于圆M,因为|NM|+|NF|=4>|FM|,所以点N的轨迹E为椭圆,且,所以b=1,所以轨迹E的方程为.…(4分)(Ⅱ)(i)当AB为长轴(或短轴)时,依题意知,点C就是椭圆的上下顶点(或左右顶点),此时|AB|=2.…(5分)(ii)当直线AB的斜率存在且不为0时,设其斜率为k,直线AB的方程为y=kx,联立方程得,所以|OA|2=.…(7分)由|AC|=|CB|知,△ABC为等腰三角形,O为AB的中点,OC⊥AB,所以直线OC的方程为,由解得,=,,…(9分)S△ABC=2S△OAC=|OA|×|OC|=,由于,由于,所以,…(11分)当且仅当1+4k2=k2+4,即k=±1时等号成立,此时△ABC面积的最小值是,因为,所以△ABC面积的最小值为,此时直线AB的方程为y=x或y=﹣x.直线与椭圆的位置关系问题:12211||.lyyk忆一忆知识要点④可通过根与系数的关系来解决中点弦问题;这其中的解题方法就是常说的“设而不求,整体代入”;⑤忆一忆知识要点