直线与圆的会考复习课件VIP免费

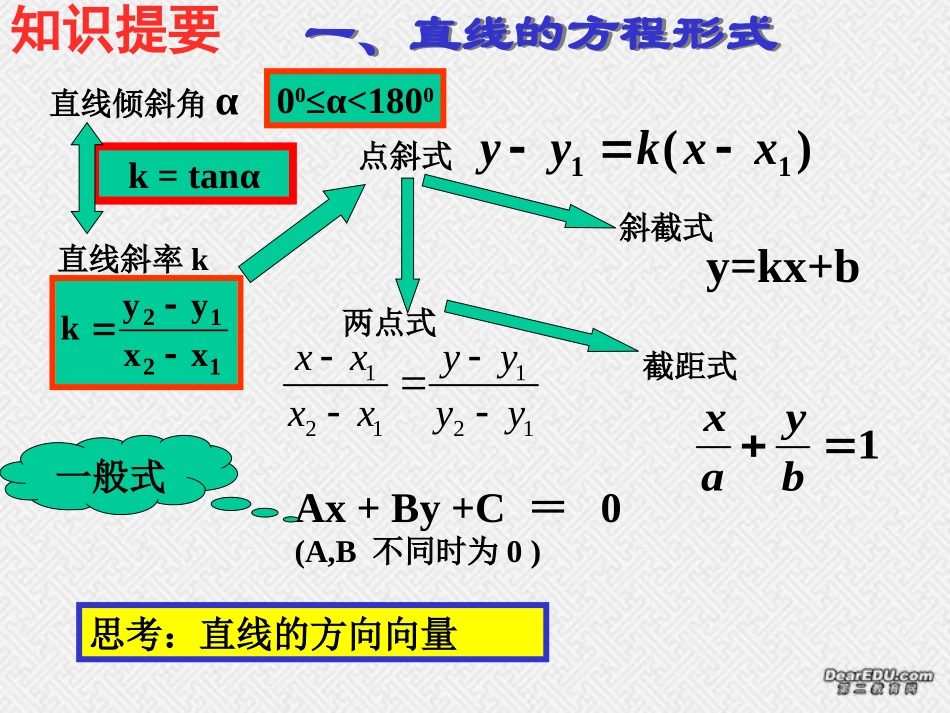
k=tanα直线斜率k直线倾斜角α1212xxyyky=kx+b)(11xxkyy112121xxyyxxyy1byax点斜式斜截式两点式截距式00≤α<1800Ax+By+C＝0(A,B不同时为0)一般式一、直线的方程形式一、直线的方程形式思考：直线的方向向量知识提要二、两直线的位置关系二、两直线的位置关系k1=k2且b1≠b21、平行2、垂直k1·k2=-1若直线l1:A1x+B1y+C1=0，直线l2:A2x+B2y+C2=0注1：则l1⊥l2A1A2+B1B2=0当A1，A2，B1，B2全不为0时，11112222//ABCllABC11112222ABCllABC、重合111222ABllAB、相交(考虑直线斜率均存在)知识提要1、与直线Ax+By+C1=0平行的直线方程：Ax+By+C2=0（C1≠C2）注2：2、与直线Ax+By+C1=0垂直的直线方程：Bx-Ay+C2=03、过l1:A1x+B1y+C1=0，l2:A2x+B2y+C2=0交点的直线系方程：A1x+B1y+C1+λ(A2x+B2y+C2)=0k1=k2且b1≠b21、平行2、垂直k1·k2=-1(考虑直线斜率均存在)二、两直线的位置关系二、两直线的位置关系知识提要l1l2θ00≤θ<180021121tankkkk3、l1到l2的角θ4、l1与l2的夹角α（l1与l2所成的角）00≤α≤90021121tankkkk知识提要二、两直线的位置关系二、两直线的位置关系5、点到直线的距离：点P(x0,y0)到直线L:Ax+By+C=0的距离公式：2200BA|CByAx|d1222CCdAB两条平行线Ax+By+C1=0与Ax+By+C2=0的距离为知识提要二、两直线的位置关系二、两直线的位置关系知识提要在平面直角坐标系中，不等式Ax+By+C>0表示在直线：Ax+By+C=0的某一侧的平面区域xyoAx+By+C=0①②1.二元一次不等式表示平面区域判断方法：直线定界，特殊点定域知识提要应该注意的几个问题：应该注意的几个问题：1、若Ax+By+C>0(或<0),则边界应画成虚线，若Ax+By+C≥0(或≤0),则边界应画成实线2、画图时应非常准确，否则将得不到正确结果设z=2x+y且变量x、y满足下列条件求z的最大值和最小值由x，y的不等式(或方程)组成的不等式组称为x，y的约束条件。关于x，y的一次不等式或方程组成的不等式组称为x，y的线性约束条件。欲达到最大值或最小值所涉及的变量x，y的解析式称为目标函数。关于x，y的一次目标函数称为线性目标函数4335251xyxyx2.简单的线性规划有关概念有关概念知识提要设z=2x+y且变量x、y满足下列条件求z的最大值和最小值4335251xyxyx2.简单的线性规划有关概念有关概念知识提要求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。满足线性约束条件的解（x，y）称为可行解。所有可行解组成的集合称为可行域。使目标函数取得最大值或最小值的可行解称为最优解解线性规划问题的步骤：（2）移：在线性目标函数所表示的一组平行线中，利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线；（3）求：通过解方程组求出最优解；（4）答：作出答案（1）画：画出线性约束条件所表示的可行域；知识提要1、圆的标准方程(x-a)2+(y-b)2=r22、圆的一般方程022FEyDxyx0422FED)(,sincos为参数rbyrax3、圆的参数方程4、两个重要的直角三角形：②涉及圆的切线长时：·MPC①涉及圆的弦长时：·ABCD()2DE圆心，-2知识提要方法一：几何法直线：Ax+By+C=0;圆:(x-a)2+(y-b)2=r2，圆心到直线的距离d=知识提要5、直线与圆的位置关系方法二：判别式法直线：Ax+By+C=0;圆：x2+y2+Dx+Ey+F=0一元二次方程知识提要6、圆与圆的位置关系圆与圆位置关系的判定方法：几何法设两圆的半径分别为R和r(R>r),圆心距为d，那么：(5)两圆内含(5)两圆内含(4)两圆内切(4)两圆内切(3)两圆相交(3)两圆相交(2)两圆外切(2)两圆外切(1)两圆外离(1)两圆外离d>R+rd>R+rd=R+rd=R+rR-r