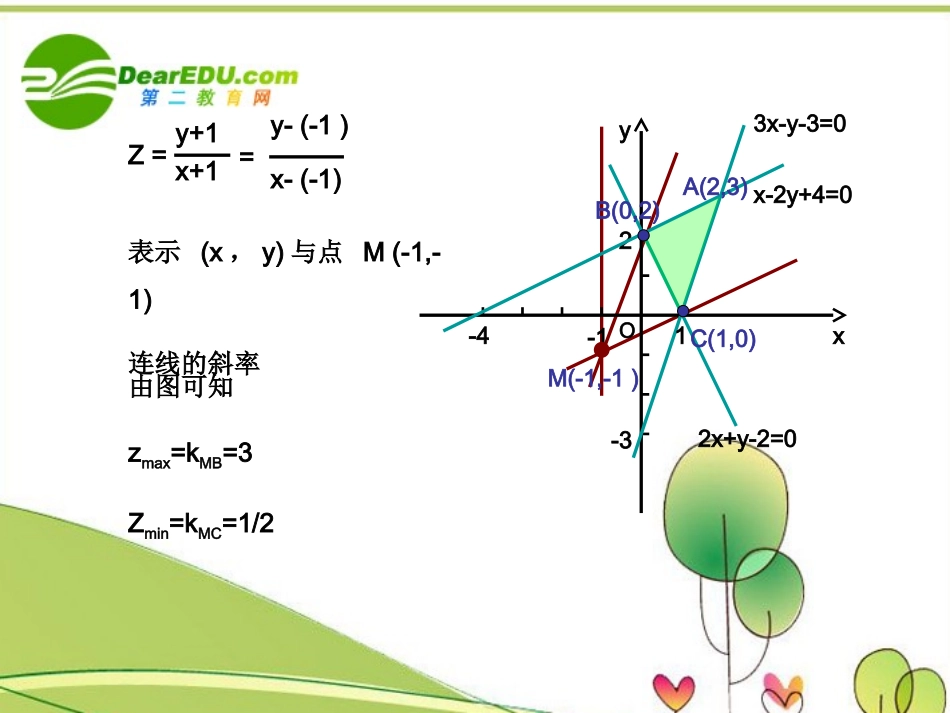
3.3.2简单的线性规划问题非线性目标函数的最值例1实数x、y满足2x+y-2≥0x-2y+4≥03x-y-3≤0①求z=y+1x+1的最值②求z=x2+y2的最值y+1x+1=y-(-1)x-(-1)Z=表示(x,y)与点M(-1,-1)连线的斜率由图可知zmax=kMB=3Zmin=kMC=1/2xyO12-3-42x+y-2=0x-2y+4=03x-y-3=0-1M(-1,-1)C(1,0)B(0,2)A(2,3)xyO12-3-42x+y-2=0x-2y+4=03x-y-3=0-1C(1,0)B(0,2)A(2,3)z=x2+y2=(x-0)2+(y-0)2表示(x,y)与点O(0,0)的距离的平方由图可知原点到A点的距离最大,到BC的距离最小zmax=︱OA︱2=13Zmin==22212200254练实数x、y满足2x+y-5≥03x-y-5≤0x-2y+5≥0①求z=yx的最值②求z=(x-1)2+y2的最值业实数x、y满足x+y-1≤0x-y+1≥0y≥-1①求z=y+4x+3的最值②求z=(x-2)2+(y-2)2的最值反思:由于学生对正切函数图像、直线的倾斜角、斜率、两点间距离公式、点到直线的距离公式遗忘、所以讲起来非常慢。学生理解起来特别费劲。正课只讲了例1,副课讲了二十分钟练习,剩二十分钟做作业