高考数学复习 平面几何训练 ppt 试题VIP免费

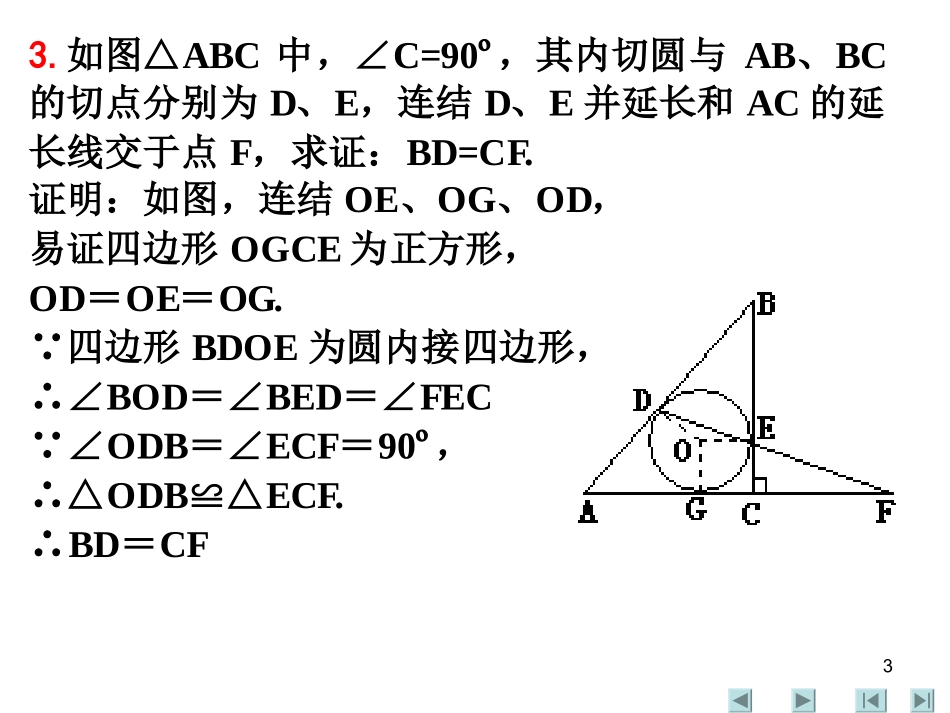
11.如果边长顺次为25，39，52和60的四边形内接于一圆，那么此圆的周长为()(A)62π(B)63π(C)64π(D)65π2.ABC△的三边长分别为5、6、7，P是ABC△内的任意一点,则PAPBPC的最小值为______.3.如图△ABC中，∠C=90º，其内切圆与AB、BC的切点分别为D、E，连结D、E并延长和AC的延长线交于点F，求证：BD=CF.4.AD是ABC△的外接圆O的直径,过D作圆O的切线交BC于P,连接并延长PO分别交AB、AC于M、N，求证:OM=ON.5.如图,在锐角△ABC的BC边上有两点E,F,满足BAECAF,作FMABM于,作FNACN于,延长AE交△ABC的外接圆于点D,求证:四边形AMDN与△ABC的面积相等.1答案2答案3答案平面几何训练22.解:易知△ABC是锐角三角形，存在点O在△ABC内120AOBBOCCOA如图P是△ABC内的任意一点，则PAPBPCOAOBOC≥,不妨设5,6,7ACABBC∵ACOAOBOC（如图），易求265sin,cos77BB，∴2267267cos(60)55362ACB1.如图，设ABCD为圆内接四边形，且AB=25，BC=39，CD=52，DA=60由圆内接四边形对角互补得∠C=180º－∠A连结BD，在△ABD与△BCD中,由余弦定理,得:2222cosBDABADABADA＝222cosCBCDCBCDC即22256022560cosA＝22395223952cosA解得cos∠A=0∴∠A=90º，故BD为圆的直径∴65602522BD∴圆的周长为65πDCBA33.如图△ABC中，∠C=90º，其内切圆与AB、BC的切点分别为D、E，连结D、E并延长和AC的延长线交于点F，求证：BD=CF.证明：如图，连结OE、OG、OD，易证四边形OGCE为正方形，OD＝OE＝OG.∵四边形BDOE为圆内接四边形，∴∠BOD＝∠BED＝∠FEC∵∠ODB＝∠ECF＝90º，∴△ODB≌△ECF.∴BD＝CF44.AD是△ABC的外接圆O的直径,过D作圆O的切线交BC于P,连接并延长PO分别交AB、AC于M、N，求证:OM=ON.55.如图,在锐角△ABC的BC边上有两点E,F,满足BAECAF,作FMABM于,作FNACN于,延长AE交△ABC的外接圆于点D,求证:四边形AMDN与△ABC的面积相等.(2000全国高中联赛题)