高二数学：(椭圆及标准方程)课件旧人教版 课件VIP免费

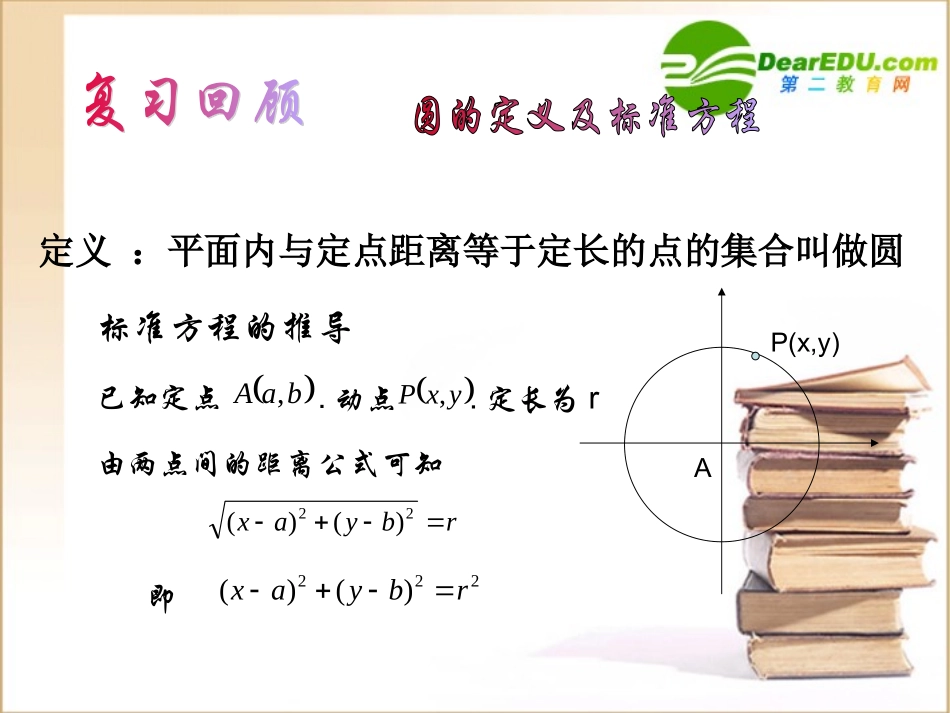
及其标准方程及其标准方程定义：平面内与定点距离等于定长的点的集合叫做圆标准方程的推导已知定点baA,.动点yxP,.定长为r由两点间的距离公式可知rbyax22)()(即222)()(rbyaxAP(x,y)圆是与一定点的距离等于定长的点的集合。那么又是什么图形呢？与两定点的距离之和为一定长的点的集合固定两个点然后我们来做一个实验。在一个木棍上用两个钉子21FF,取一条定长L的细绳,使它的两端固定在21FF,上，用铅笔绷住细绳使它慢慢移动，它得到的图形，我们叫它定义为椭圆。由上述的画图过程可知椭圆是与的距离的和等于定长的集合21FF,oxy1F2F汽车贮油罐的横截面的外轮廓线的形状像椭圆.把一个圆压扁了,也像椭圆思考怎样判定它们就是椭圆呢?1.根据椭圆的定义2.根据椭圆的方程定义椭圆标准方程xyOF1F2M取过焦点F1,F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系.（如图）把坐标代入方程:|MF1|+|MF2|=2a得：则椭圆就是集合：P={M||MF1|+|MF2|=2a}．设M(x,y)为椭圆上任意一点,椭圆焦距为2c(c>0),M到F1和到F2的距离之和等于正数2a,F1,F2的坐标分别为（-c,0），（c,0）．平面内到两定点的距离等于定长2a(>|F1F2|）的点的轨迹称椭圆．两定点称焦点，|F1F2|称焦距．移项，两边平方得2222222)()(44)(ycxycxaaycx两边再平方得:2222222222422yacacxaxaxccxaa整理得)()(22222222caayaxca由椭圆定义可知:2a>2c,即a>c,所以设,0ca22得两边除以22222222,babayaxb12222byax)0b(bca222a2y)cx(y)cx(2222222y)cx(acxa它所表示的椭圆焦点在x轴上,分别为:F1(-c,0),F2(c,0)．椭圆标准方程xyOF1F2M)0(12222babyax焦点F1(-c,0),F2(c,0)在x轴上若椭圆焦点F1(0,-c),F2(0,c)在y轴上，因为这时x轴与y轴交换,所以只要把方程中的x,y互换即可得方程:)0ba(1bxay2222焦点F1(0,-c),F2(0,c)在y轴上xyOF2F1M其中:a2-c2=b21.根据已知条件，求下列椭圆的焦点坐标1.根据已知条件，求下列椭圆的焦点坐标14922yx(1)11271622yx(2)2.求适合下列条件的椭圆的标准方程1)两个焦点的坐标分别是(-4,0)、(4,0)，椭圆上一点到两焦点距离的和等于10；2)两个焦点的坐标分别是(0,-2)、(0,2)并且经过点；例1：已知B，C是两个定点，|BC|=6，且三角形ABC的周长为16，求顶点A的轨迹方程．解：1)建立直角坐标系：使x轴经过点B、C，使原点O与B、C重合B（-3，0），C（3，0）2)设A点的坐标为（x，y）由|AB|+|AC|+|BC|=16，|BC|=6，即|AB|+|AC|=10BC（用轨迹法）10y)3x(y)3x(2222O化简可得方程：A当点A在直线BC上，即y=0时，A、B、C三点不能构成三角形．所以A点的轨迹方程为：116y25x22116y25x22（y0）．xy解：例2:将圆=4上的点的横坐标保持不变，纵坐标变为原来的一半，求所的曲线的方程，并说明它是什么曲线？yxo22yx设所的曲线上任一点的坐标为(x，y),圆＝４上的对应点的坐标为（x’，y’），由题意可得：22yxyyxx2//22yx因为＝４所以4422yx即1422yx1）将圆按照某个方向均匀地压缩（拉长），可以得到椭圆。2）利用中间变量求点的轨迹方程的方法是解析几何中常用的方法；例3:已知一个运油车上的贮油罐横截面的外轮廓线是一个椭圆，它的焦距为2.4m，外轮廓线上的点到两个焦点距离的和为3m，求这个椭圆的标准方程．解：以两焦点F1、F2所在直线为x轴，线段F1F2的垂直平分线为y轴，建立如图所示的直角坐标系xOy，则这个椭圆的标准方程可设为222210xyabab根据题意有23a，22.4c1.5a，1.2c即222221.51.20.81bac因此，这个椭圆的标准方程为2212.250.81xyxyOF1F22222+=1>>0xyabab2222+=1>>0xyabba分母哪个大，焦点就在哪个轴上平面内到两个定点F1，F2的距离的和等于常数（大于F1F2）的点的轨迹12-,0,0，FcFc120,-0,，FcFc标准方程相同点焦点位置的判断不同点图形焦点坐标定义a、b、c的关系根据所学知识完成下表xyF1F2POxyF1F2POa2-c2=b2思考题xyP(-3,0)Q(3,0)oAM已知定圆⊙Q:x2+y2-6x-55=0,动圆⊙M和已知定圆内切于点A且过点P(-3,0),求圆心M的轨迹及其方程答案：圆心M的轨迹为椭圆；方程为：17y16x22