概率的加法公式 高二数学概率知识的课件集合 人教版 高二数学概率知识的课件集合 人教版VIP免费

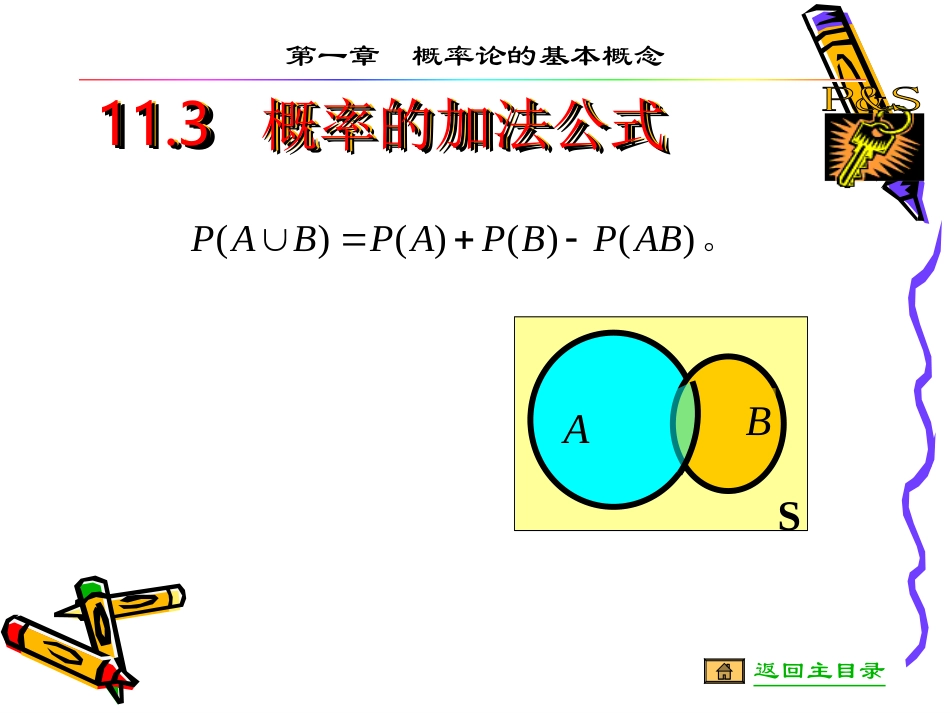
。)()()()(ABPBPAPBAPSAB第一章概率论的基本概念返回主目录11.311.3概率的加法公式概率的加法公式11.311.3概率的加法公式概率的加法公式)()()()()()()()()1ABCPBCPACPABPCPBPAPCBAP第一章概率论的基本概念返回主目录nAAAPnnkjikAjAiAPnjijAiAPniiAPniiAPnAAAn21111111,,,2,1)2有个事件对任意加法公式的推广例1小王参加“智力大冲浪”游戏,他能答出甲、乙二类问题的概率分别为0.7和0.2,两类问题都能答出的概率为0.1.求小王解事件A,B分别表示“能答出甲,乙类问题”(1)6.01.07.0)()()(ABPAPBAP(1)答出甲类而答不出乙类问题的概率(2)至少有一类问题能答出的概率(3)两类问题都答不出的概率(2)8.0)()()()(ABPBPAPBAP(3)2.0)()(BAPBAP课后同学问：例1中小王他能答出第一类问题的概率为0.7,答出第二类问题的概率为0.2,两类问题都能答出的概率为0.1.为什么不是？2.07.0若是的话,则应有)()()(2121APAPAAP而现在题中并未给出这一条件.在§1.4中将告诉我们上述等式成立的条件是：事件相互独立.21,AA例2设A,B满足P(A)=0.6,P(B)=0.7,在何条件下，P(AB)取得最大(小)值？最大(小)值是多少？解)()()()(ABPBPAPBAP)()()()(BAPBPAPABP3.01)()(BPAP1)(BAP最小值在时取得6.0)()(APABP——最小值——最大值)()(BPBAP最大值在时取得课上有同学提问最小值是否正确？例2中回答当时,取得BA)(BAP这相当于问如下命题是否成立答：不成立！BA1)(BAP⊛⊛式是“羊肉包子打狗”——有去路,没回路为什么呢？学了几何概型便会明白.