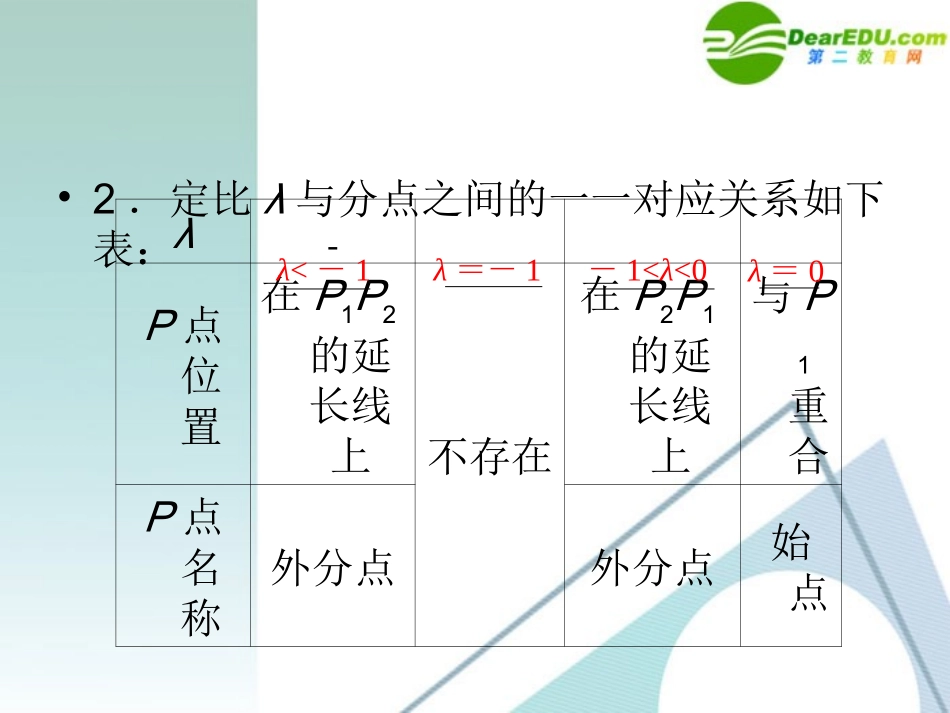
•●基础知识•一、线段的定比分点•1.定比分点:设P1,P2是直线l上的两点,点P是l上不同于P1,P2的任意一点,则存在一个实数λ,使=•,λ叫点P分有向线段所成的比,P叫做.定比分点•2.定比λ与分点之间的一一对应关系如下表:λP点位置在P1P2的延长线上不存在在P2P1的延长线上与P1重合P点名称外分点外分点始点λ<-1λ=-1-1<λ<0λ=0λP点位置在P1与中点之间P为中点在中点与P2之间P点名称内分点0<λ<1λ=1λ>1•3.线段定比分点坐标公式•设点P分有向线段所成的比为λ,即•并且P1(x1,y1),P2(x2,y2),P(x,y),则•这就是有向线段的定比分点坐标公式.特别地,当P是的中点时,•二、图形的平移•1.平移•设F为坐标平面内一个图形,将F上•,得到图形F′,这个过程叫图形的•.将一个图形平移,图形的不变,只是在坐标平面内的发生变化.所有点按同一个方向移动同样的长度平移形状、大小位置•2.平移公式•设P(x,y)为图形F上任一点,它按向量a=(h,k)平移后的图形F′上对应点为P′(x′,y′),则有•在P(x,y),P′(x′,y′)以及a=(h,k)中,已知其中两个,可求另外一个,但要注意顺序性.•3.函数图象的平移,实质上是,可由平移公式化简方程.点的平移•●易错知识•一、定比分点公式应用失误•失分警示:概念混淆,定比分点概念不清致误.•2.已知P1(-1,-6)、P2(3,0),在直线P1P2上取一点P,则点P的坐标为________.•二、平移公式应用失误•3.已知A(4,2),B(1,2),则向量沿向量(-1,3)平移后得到的向量坐标是________.•答案:(3,0)•4.把一个函数的图象按向量a=(3,-2)平移后得到的图象的解析式为y=log2(x+3)+2,则原函数的解析式为________.•答案:y=log2(x+6)+4•5.将函数y=2sin2x的图象按向量a的方向平移,得到函数y=2sin(2x+)+1的图象,则向量a的坐标为()•答案:B•三、函数与方程思想应用错误•6.已知向量a≠e,=1满足:对任意t∈R,恒有•A.a⊥eB.a(⊥a-e)•C.e(⊥a-e)D.(a+e)(⊥a-e)•答案:C•解题思路: ,∴a2+t2e2-2a·et≥a2-2ae+e2.• =1,∴t2-2a·et+2a·e-1≥0对任意t∈R恒成立.∴△=4(a·e)2-4(2a·e-1)≤0,•即(a·e)2-2a·e+1≤0,(a·e-1)2≤0,∴a·e=1,即a·e=e2,∴(a-e)·e=0,∴e⊥(a-e).故选C.•失分警示:误区1:不等式整理成t2-2a·et+2a·e-1≥0后,不能把a·e看作一个整体、一个参数,而忽视了该不等式对任意实数t恒成立的充要条件是△≤0,致使进入误区.•误区2:a·e=1而答案中没有这一选项,学生不会变通,把“1”看做e2,而总以为自己做错而选不出正确选项.•启示:函数与方程思想贯穿于整个中学数学,则向量模的关系转化为解不等式,再由解不等式探求不等式成立的条件,再由a·e=1,即便没有考虑到“1”即e2,可代入验证.•●回归教材•1.已知点P分有向线段的比为λ,则下列结论中正确的是()•A.λ可以是任意实数•B.λ是不等于零的实数•C.当λ<-1时,点P必在的延长线上•D.当-1<λ<0时,点P在的延长线上•解析:因为点P是线段上异于P1、P2的点,λ∈R且λ≠0,-1,故A、B错;•当λ<-1时,点P在线段的延长线上;•当-1<λ<0时,点P在线段的延长线上;•当λ>0时,点P在线段上.•答案:C•2.(教材P1261题改编)直线上有A、B、C三点,如果B分AC的比为-,则()•A.B是线段AC的中点•B.A是线段BC的中点•C.C是线段AB的中点•D.B是线段AC的三等分点•解析:由题意可知,•如图所示可知选B.•答案:B•3.(2008·重庆)若过两点P1(-1,2),P2(5,6)的直线与x轴相交于点P,则点P分有向线段所成的比λ的值为()•答案:A•4.(教材P1352题改编)将点A(-4,3)按向量a=(5,-2)平移后的坐标是()•A.(9,-5)B.(-9,5)•C.(1,1)D.(-8,1)•解析:按向量平移公式计算得知应选C.•答案:C•5.把函数的图象F按向量a=(,2)平移后得函数y=2sinx的图象F′,则平移前的图象F的函数解析式为________.•解析:设平移前的图象F上的任一点为P(x,y),平移后与之对应的点为P′(x′,y′),则有• 点P′(x′,y′)在函数y=2sinx的图象上,...